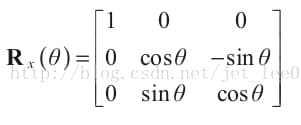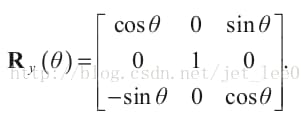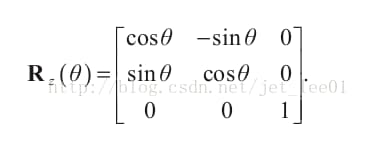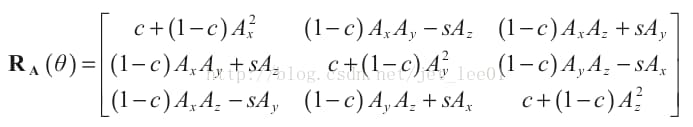Matrix

Math
2k words

矩阵

矩阵的意义

矩阵之间的计算
转置矩阵，把矩阵沿着对角线翻转一下，由于常用的是方针矩阵，所有转置后，还是相同的大小，只是将对角线两侧的数字进行对调
Image text

齐次矩阵
将一个原先是n维的矩阵用一个n+1维的矩阵表示
齐次坐标描述的是缩放不变性

矩阵可以表达空间的缩放、旋转、切边，但无法表达偏移，因此，我们增加一个维度的矩阵来表达当下维度的偏移，即齐次矩阵

旋转

旋转矩阵的推导
旋转矩阵
绕着X轴旋转的矩阵

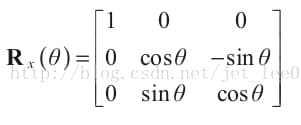
绕着Y轴旋转的矩阵

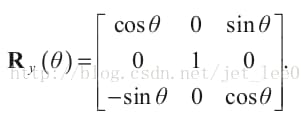
绕着Z轴旋转的矩阵

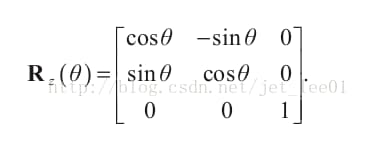
绕着任意轴旋转的矩阵

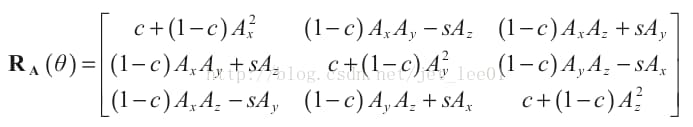
C : cosθ
S : sinθ

Game101

投影

link

Image text
Image text
Image text

从透视投影变换到正交投影的矩阵

运算

乘法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Vector3 operator*(const Vector3& v) const
{
    Vector3 r;
    float inv_w = 1.0f / (m_mat[3][0] * v.x + m_mat[3][1] * v.y + m_mat[3][2] * v.z + m_mat[3][3]);
    r.x = (m_mat[0][0] * v.x + m_mat[0][1] * v.y + m_mat[0][2] * v.z + m_mat[0][3]) * inv_w;
    r.y = (m_mat[1][0] * v.x + m_mat[1][1] * v.y + m_mat[1][2] * v.z + m_mat[1][3]) * inv_w;
    r.z = (m_mat[2][0] * v.x + m_mat[2][1] * v.y + m_mat[2][2] * v.z + m_mat[2][3]) * inv_w;
    return r;
}
Vector4 operator*(const Vector4& v) const
{
    return Vector4(m_mat[0][0] * v.x + m_mat[0][1] * v.y + m_mat[0][2] * v.z + m_mat[0][3] * v.w,
                    m_mat[1][0] * v.x + m_mat[1][1] * v.y + m_mat[1][2] * v.z + m_mat[1][3] * v.w,
                    m_mat[2][0] * v.x + m_mat[2][1] * v.y + m_mat[2][2] * v.z + m_mat[2][3] * v.w,
                    m_mat[3][0] * v.x + m_mat[3][1] * v.y + m_mat[3][2] * v.z + m_mat[3][3] * v.w);
}

构建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void Matrix4x4::makeTransform(const Vector3& position, const Vector3& scale, const Quaternion& orientation)
{
    // Ordering:
    //    1. Scale
    //    2. Rotate
    //    3. Translate
    Matrix3x3 rot3x3;
    orientation.toRotationMatrix(rot3x3);
    // Set up final matrix with scale, rotation and translation
    m_mat[0][0] = scale.x * rot3x3[0][0];
    m_mat[0][1] = scale.y * rot3x3[0][1];
    m_mat[0][2] = scale.z * rot3x3[0][2];
    m_mat[0][3] = position.x;
    m_mat[1][0] = scale.x * rot3x3[1][0];
    m_mat[1][1] = scale.y * rot3x3[1][1];
    m_mat[1][2] = scale.z * rot3x3[1][2];
    m_mat[1][3] = position.y;
    m_mat[2][0] = scale.x * rot3x3[2][0];
    m_mat[2][1] = scale.y * rot3x3[2][1];
    m_mat[2][2] = scale.z * rot3x3[2][2];
    m_mat[2][3] = position.z;
    // No projection term
    m_mat[3][0] = 0;
    m_mat[3][1] = 0;
    m_mat[3][2] = 0;
    m_mat[3][3] = 1;
}

向量坐标转换

齐次坐标处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Vector3 transformCoord(const Vector3& v)
{
    Vector4 temp(v, 1.0f);
    Vector4 ret = (*this) * temp;
    if (ret.w == 0.0f)
    {
        return Vector3::ZERO;
    }
    else
    {
        ret /= ret.w;
        return Vector3(ret.x, ret.y, ret.z);
    }
    return Vector3::ZERO;
}