Vector

Math
2.6k words

向量

向量的意义

通常用于表示坐标数据，距离，速度，位移，加速度

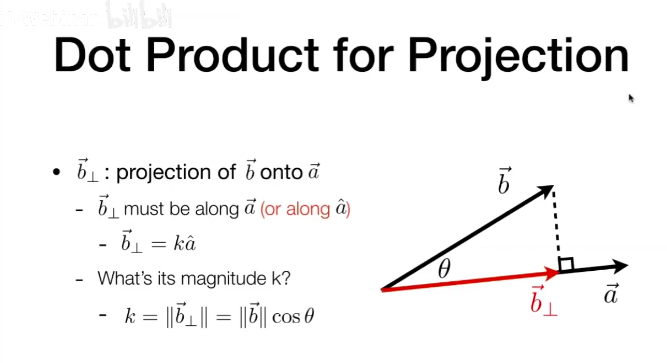
点乘

得到两向量之间的夹角
得到向量在坐标轴下的投影
两个向量之间的方向
Image text
Image text
p作为坐标系任意一个点，可以由三个相互坐标轴表示，三个轴方向的投影

Image text
Image text
Image text

1
2
3
float dotProduct(const Vector3& vec) const {
    return x * vec.x + y * vec.y + z * vec.z; 
}

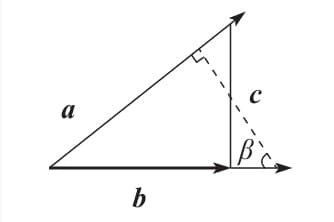
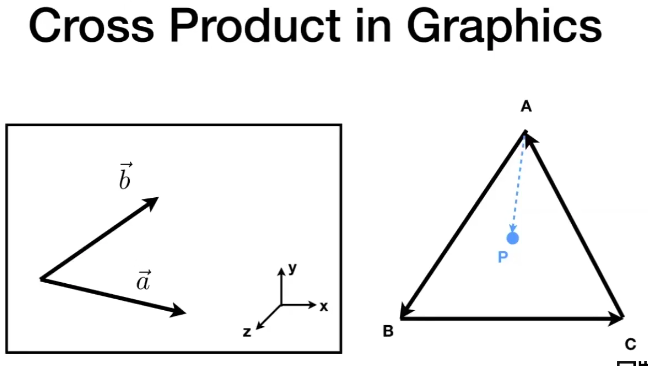
叉乘的意义

a、b向量形成的四边形的面积值
Vector3.Cross
Image text
可以用于判断向量的左右关系，和点在多边形内外
Image text

角度计算

1
2
3
4
5
6
7
8
9
10
11
Radian angleBetween(const Vector3& dest) const
{
    float len_product = length() * dest.length();
    // Divide by zero check
    if (len_product < 1e-6f)
        len_product = 1e-6f;
    float f = dotProduct(dest) / len_product;
    f = Math::clamp(f, (float)-1.0, (float)1.0);
    return Math::acos(f);
}

万向锁问题

万向锁问题是在使用欧拉角进行旋转时会出现的一种现象，它会导致在某些方向上的旋转失效，因为这个方向会和另一个轴的旋转产生冲突。解决万向锁问题的方法通常有以下几种

  1. 使用四元数进行旋转：四元数可以避免万向锁问题，而且在插值和累积旋转方面更加高效和精确（相对于使用矩阵转换来说，会减少浮点数运算次数，矩阵旋转还会存在万向锁的问题）
  2. 使用轴角表示进行旋转：轴角表示也可以避免万向锁问题，其表示方式是使用一个轴向量和一个角度来表示旋转
  3. 使用角度限制：可以对旋转的角度进行限制，比如在某个轴向上旋转的角度不超过90度。这种方法可以避免万向锁问题，但是可能会产生其他问题，比如旋转不连续
  4. 避免连续旋转：避免在同一个轴向上进行连续旋转，可以使用其他轴进行旋转。如果需要在同一个轴向上进行连续旋转，可以使用微小的偏移量或者随机化来避免万向锁问题(Unity中对于摄像机旋转，就可以做如下处理，将摄像机置于一个空物体下，控制空物体的水平轴旋转带动摄像机旋转，垂直旋转时旋转摄像机自身)

得到旋转的四元数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
Quaternion getRotationTo(const Vector3& dest, const Vector3& fallback_axis = Vector3::ZERO) const
{
    // Based on Stan Melax's article in Game Programming Gems
    Quaternion q;
    // Copy, since cannot modify local
    Vector3 v0 = *this;
    Vector3 v1 = dest;
    v0.normalise();
    v1.normalise();
    float d = v0.dotProduct(v1);
    // If dot == 1, vectors are the same
    if (d >= 1.0f)
    {
        return Quaternion::IDENTITY;
    }
    if (d < (1e-6f - 1.0f))
    {
        if (fallback_axis != Vector3::ZERO)
        {
            // rotate 180 degrees about the fall back axis
            q.fromAngleAxis(Radian(Math_PI), fallback_axis);
        }
        else
        {
            // Generate an axis
            Vector3 axis = Vector3::UNIT_X.crossProduct(*this);
            if (axis.isZeroLength()) // pick another if collinear
                axis = Vector3::UNIT_Y.crossProduct(*this);
            axis.normalise();
            q.fromAngleAxis(Radian(Math_PI), axis);
        }
    }
    else
    {
        float s    = Math::sqrt((1 + d) * 2);
        float invs = 1 / s;
        Vector3 c = v0.crossProduct(v1);
        q.x = c.x * invs;
        q.y = c.y * invs;
        q.z = c.z * invs;
        q.w = s * 0.5f;
        q.normalise();
    }
    return q;
}

反射

推导

1
2
3
4
5
6
7
/** Calculates a reflection vector to the plane with the given normal .
@remarks NB assumes 'this' is pointing AWAY FROM the plane, invert if it is not.
*/
Vector3 reflect(const Vector3& normal) const
{
    return Vector3(*this - (2 * this->dotProduct(normal) * normal));
}

投影

1
2
3
Vector3 project(const Vector3& normal) const { 
    return Vector3(*this - (this->dotProduct(normal) * normal));
}

插值运算

1
2
3
4
5
6
7
8
static Vector3 lerp(const Vector3& lhs, const Vector3& rhs, float alpha) { 
    return lhs + alpha * (rhs - lhs);
    }

static Vector3 clamp(const Vector3& v, const Vector3& min, const Vector3& max)
{
    return Vector3(Math::clamp(v.x, min.x, max.x), Math::clamp(v.y, min.y, max.y), Math::clamp(v.z, min.z, max.z));
}