空间数据结构

空间数据结构
24k words

空间数据结构

在游戏程序中，利用空间数据结构加速计算往往是非常重要的优化思想，空间数据结构可以应用于场景管理、渲染、物理、游戏逻辑等方面
link
19.1 空间数据结构 - Justin的文章 - 知乎

四叉树/八叉树

四叉树索引的基本思想是将地理空间递归划分为不同层次的树结构。
它将已知范围的空间等分成四个相等的子空间，如此递归下去，直至树的层次达到一定深度或者满足某种要求后停止分割

松散四叉树/八叉树：解决边界问题


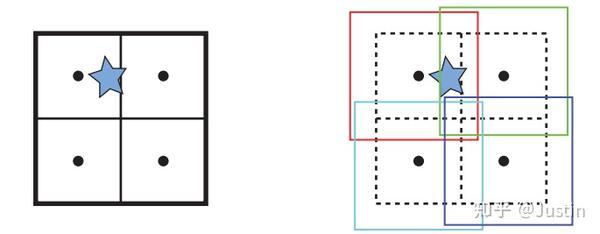
四叉树/八叉树的一个问题是，物体有可能在边界处来回，从而导致物体总是在切换节点，从而不得不更新四叉树/八叉树。

而松散四叉树/八叉树正是解决这种边界问题的一种方式：
首先它定义一个节点有入口边界(inner boundary)，出口边界(outerboundary)。
那么如何判定一个物体现在在哪个节点呢？

若物体还没添加进四叉树/八叉树，则检测现在位于哪个节点的入口边界内;
若物体先前已经存在于某个节点，则先检测现在是否越出该节点的出口边界，若越出再检测位于哪个节点的入口边界内。
在非松散的四叉树/八叉树中，入口边界和出口边界是一样的。
而松散四叉树/八叉树的松散，是指出口边界比入口边界要稍微宽些（各节点的出口边界也会发生部分重叠，松散比较符合这种描述），从而使节点不容易越过出口边界，减少了物体切换节点的次数

在一篇关于松散四叉树/八叉树的论文里，实验表明出口边界长度为入口边界2倍时可以表现得很好
link

应用

· 场景管理
四叉树
· 碰撞检测
不同划分区域保证不会碰撞的情况下，就能快速过滤与本物体不同区域的其他潜在物体碰撞
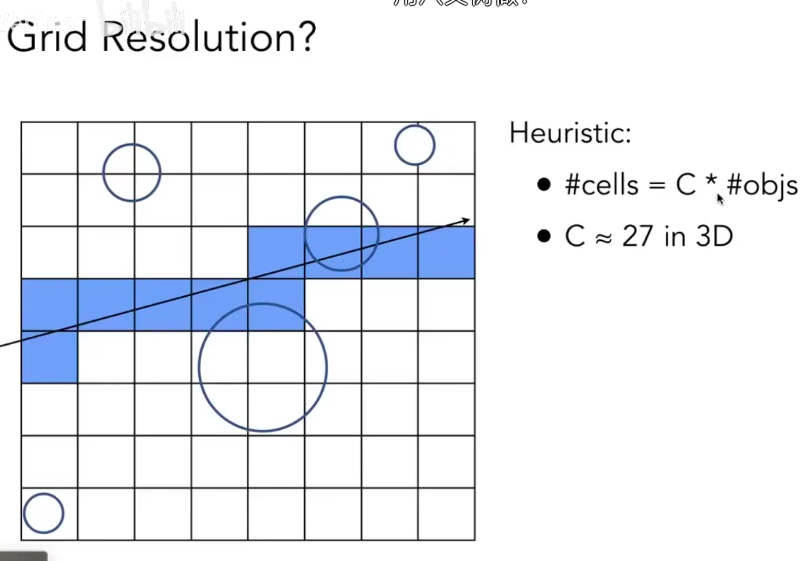
· 光线追踪
用八叉树来划分3D空间区域，从而过滤掉大量不必要的区域
四叉树实现

层次包围盒树(BVH)

层次包围盒树（BVH树）是一棵多叉树，用来存储包围盒形状。
它的根节点代表一个最大的包围盒，其多个子节点则代表多个子包围盒。

此外为了统一化层次包围盒树的形状，它只能存储同一种包围盒形状。

计算机的包围盒形状有球体/AABB/OBB/k-DOP，若不清楚这些形状术语可以自行搜索了解。

常用的层次包围盒树有AABB层次包围盒树和球体树。

AABB包围盒树

把不同形状粗略用AABB形状围起来看作一个AABB形状（为了统一化形状），然后才建立层次AABB包围盒树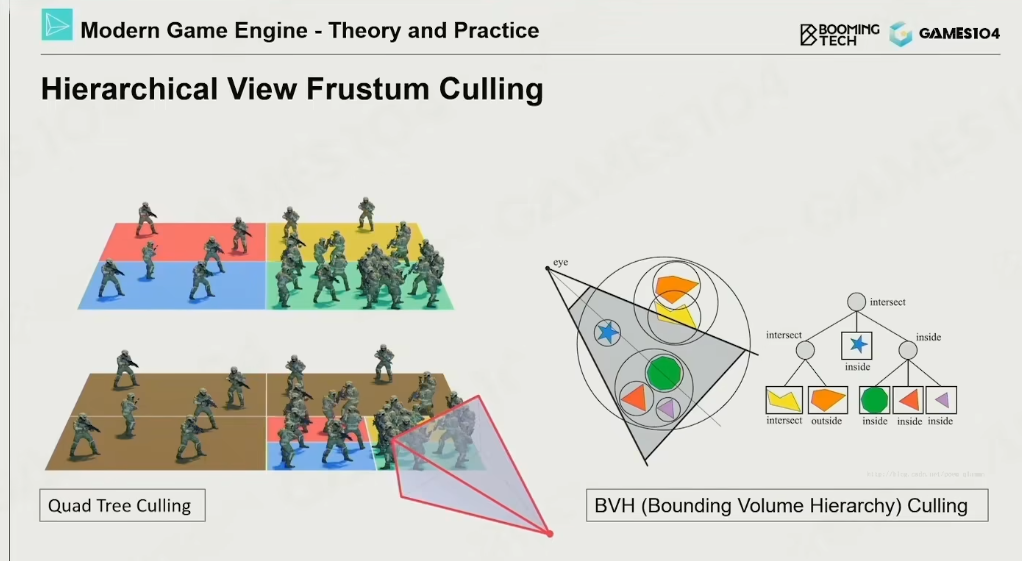
Image text
在物理引擎里，由于物理模拟，大部分形状都是会动态更新的，例如位移/旋转都会改变形状。于是就又有一种支持动态更新的层次包围盒树，称之为动态层次包围盒树。它的算法核心大概：形状的位移/旋转/伸缩更新对应的叶节点，然后一级一级更新上面的节点，使它们的包围体包住子节点
层次包围盒实现

球体包围盒树

球体是最容易计算的一类包围盒，而且球体树构造速度可以很快，因此球体树可被用作粗略松散但快速的空间划分结构(复杂物体计算圆心挺麻烦的…)

构建步骤
  1. 计算出包围所有三角边顶点的最小球体包围盒，作为根节点
  2. 以球心为坐标系原点，其坐标系X轴划分在该X轴左右的三角形，并将这些分别放入左子节点、右子节点中
  3. 重复步骤1、2，最后得到一颗球体树

在步骤2中，还可以按X轴、Y轴、Z轴的顺序轮流划分，即第一次步骤2划分用X轴，第二次步骤2划分用Y轴

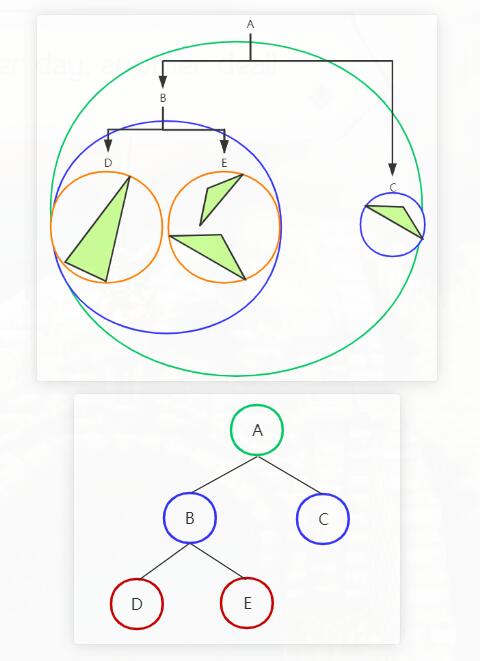
Image text
球体树粗糙，但是平衡效果不差，且它构造时间复杂度只有O(NlogN)

动态层次包围盒

构建步骤

1.构建一个初始的BVH：使用一种构建算法（例如SAH、Binned SAH等），将所有物体递归地分割成较小的组，并将这些组放入树中的叶子节点中。在这个过程中，您需要为每个节点计算它所包含的物体的包围盒
2.监听物体变化：如果您的应用程序中的物体是动态的，那么您需要能够监听它们的变化（例如，当物体的位置或形状发生变化时）。一旦发现这些变化，您需要执行下面的步骤
3.更新叶节点：找到包含被修改物体的叶节点，并更新它的包围盒。这可能会导致该节点的父节点和祖先节点的包围盒也需要更新
4.展开树：从被修改物体的叶节点开始，展开整个树，一直到根节点。对于每个节点，您需要计算其子节点的包围盒，然后更新该节点的包围盒。这可能会导致该节点的父节点和祖先节点的包围盒也需要更新
5.重建树：如果在展开树的过程中发现某些节点不再满足BVH的质量标准（例如，SAH或Binned SAH），则需要对这些节点进行重建。重建过程涉及到递归地将节点分割成更小的组，并创建新的节点来替换旧节点

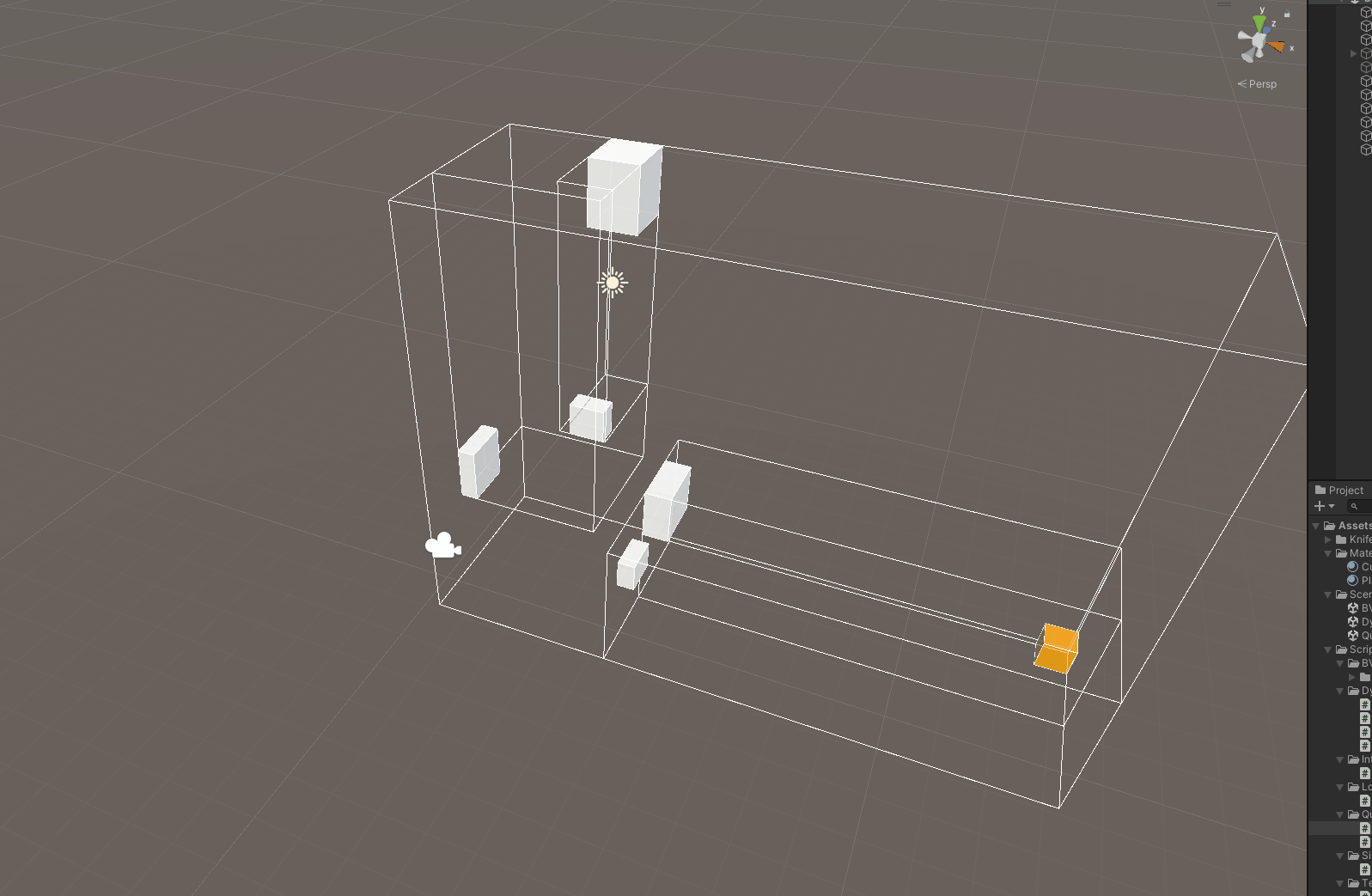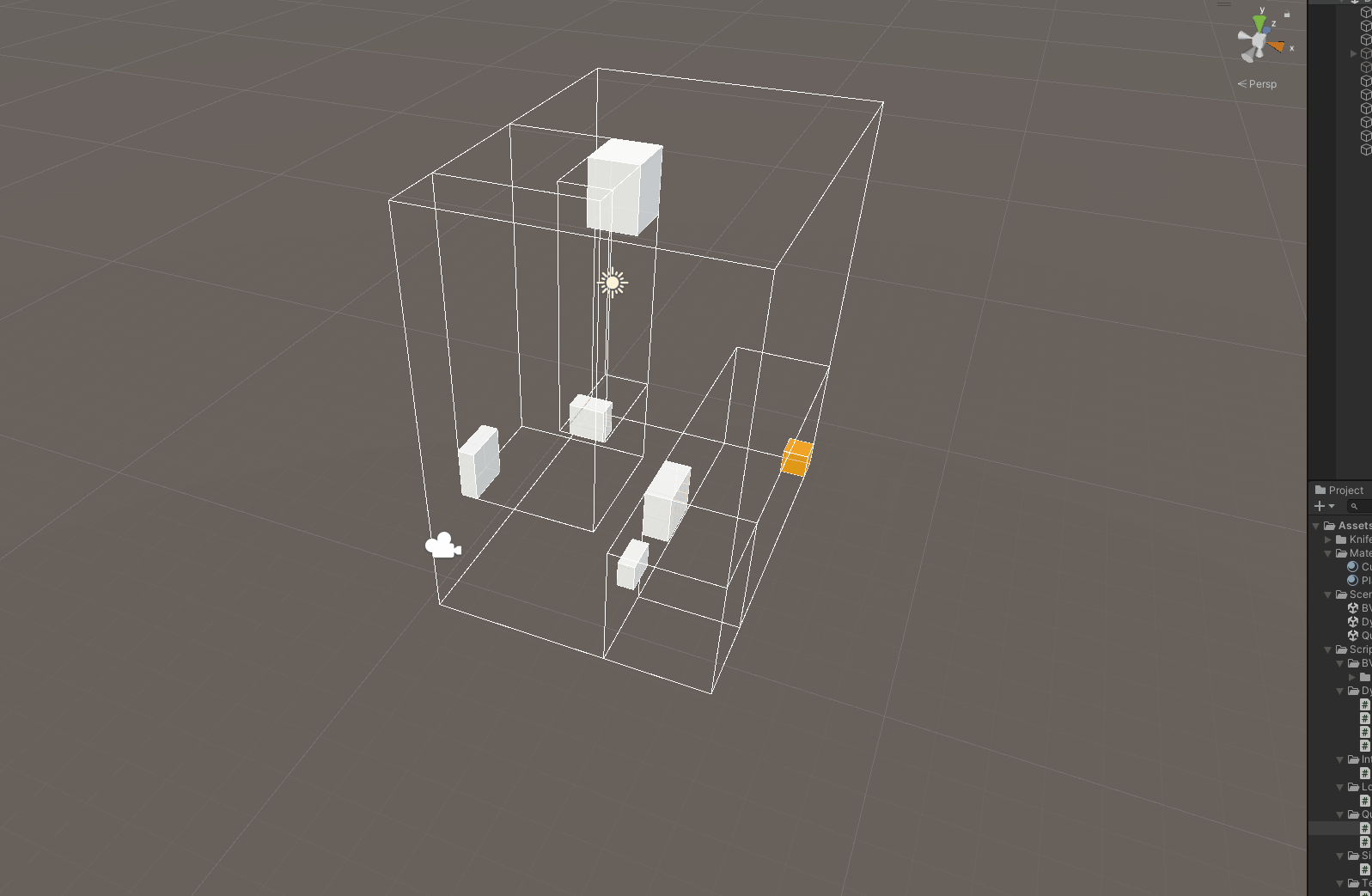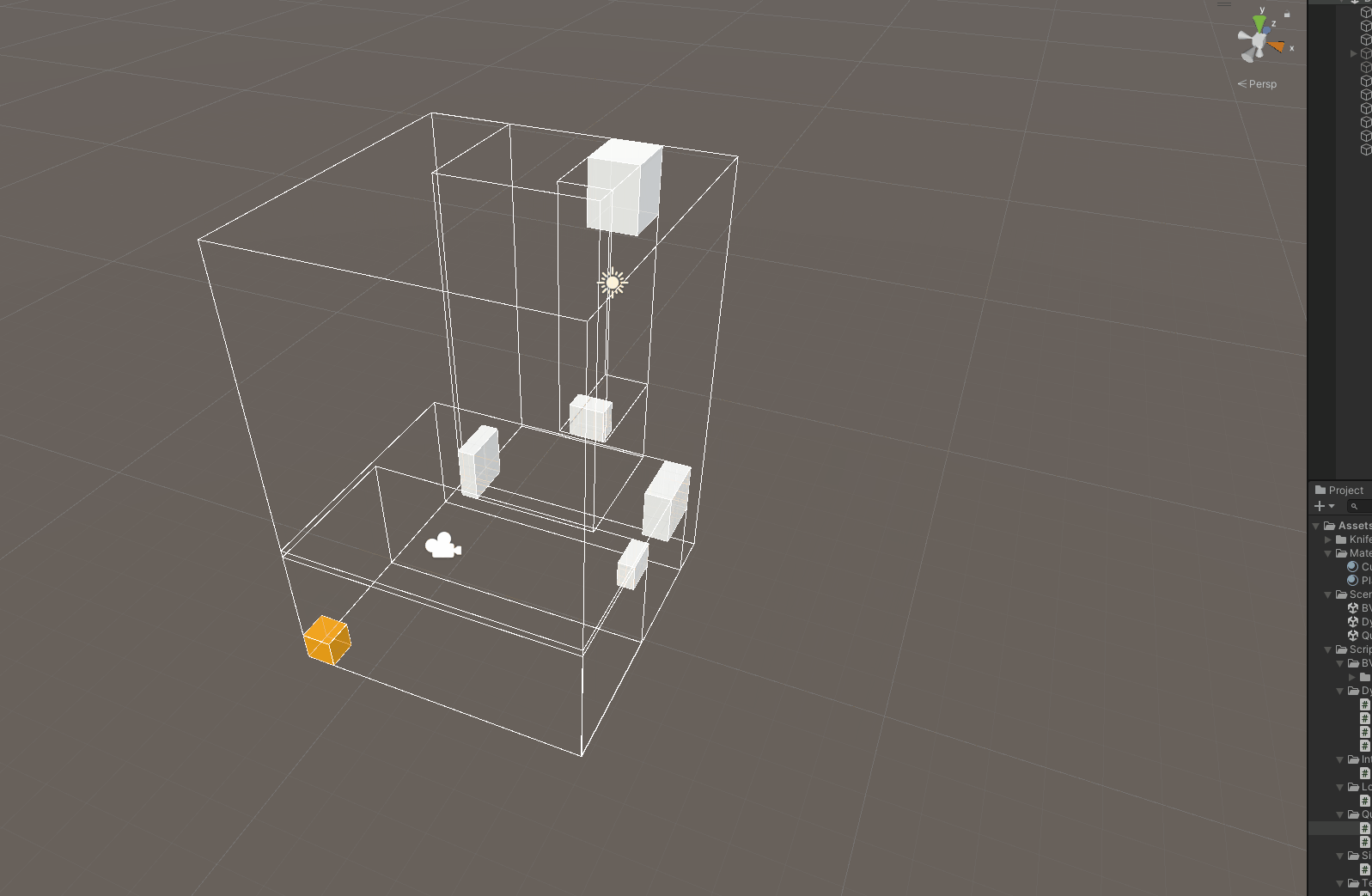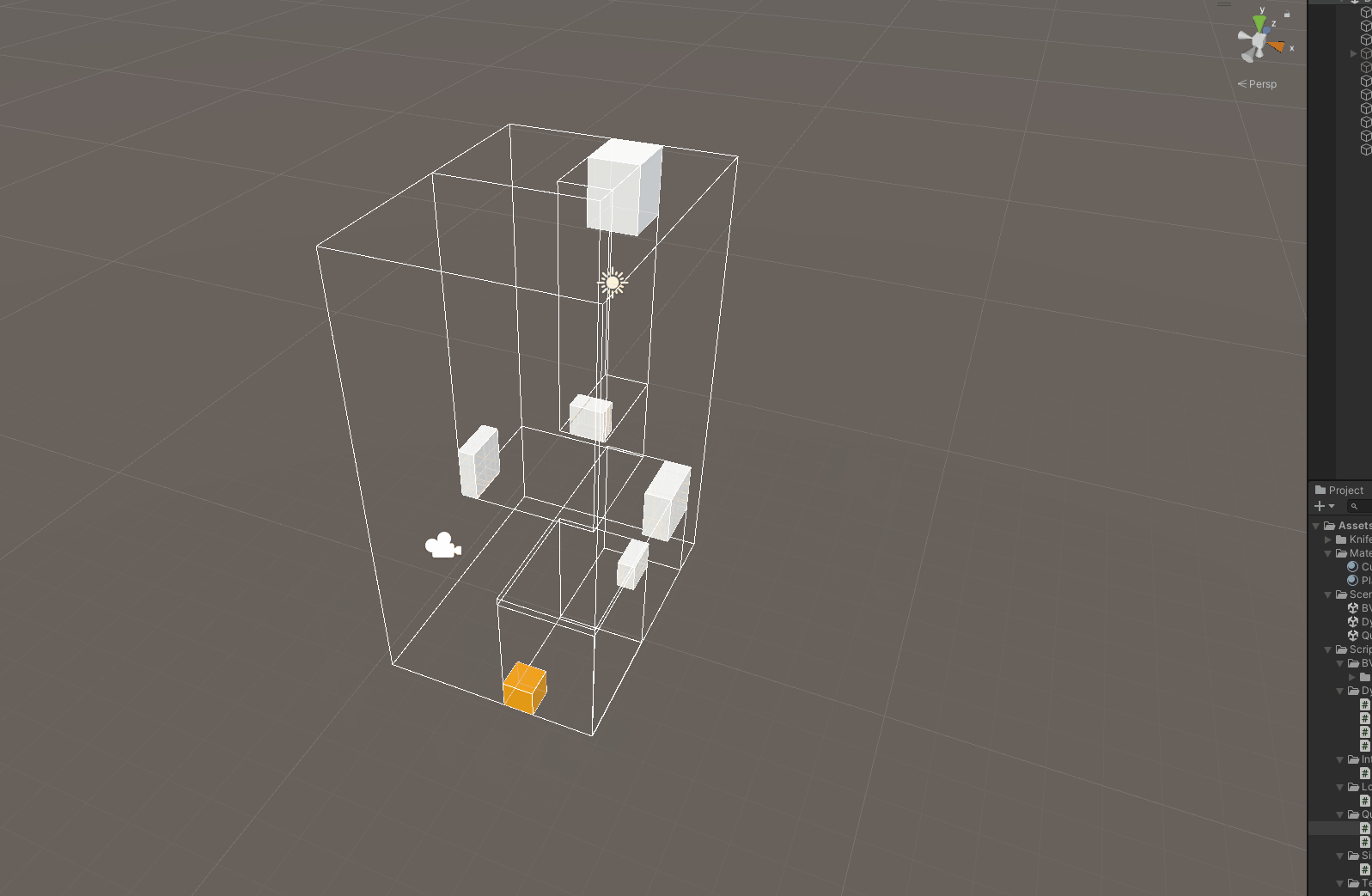
Image text

节点的添加 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

private void InsertNode(Node node)
{
    if (root == null)
    {
        root = node;
        return;
    }
    InsertNode(root, node);
}

private void InsertNode(Node node, Node newNode)
{
    if (node.isLeaf)
    {
        Node newParent = new Node();
        newParent.parent = node.parent;

        newNode.parent = newParent;
        if (root == node)
        {
            root = newParent;
        }
        else
        {
            if (node.parent.left == node)
            {
                node.parent.left = newParent;
            }
            else if (node.parent.right == node)
            {
                node.parent.right = newParent;
            }
        }
        node.parent = newParent;

        newParent.left = node;
        newParent.right = newNode;

        newParent.aabb = AABB.CreateByAABB(node.aabb, newNode.aabb);
        Node parent = newParent.parent;
        while (parent != null)
        {
            parent.UpdateAABB();
            parent = parent.parent;
        }

    }
    else if (node.left == null)
    {
        node.left = newNode;
        newNode.parent = node;
        Node parent = newNode.parent;
        while (parent != null)
        {
            parent.UpdateAABB();
            parent = parent.parent;
        }
    }
    else if (node.right == null) {
        node.right = newNode;
        newNode.parent = node;
        Node parent = newNode.parent;
        while (parent != null)
        {
            parent.UpdateAABB();
            parent = parent.parent;
        }
    }
    else
    {
        AABB combinedAABB = AABB.CreateByAABB(node.aabb, newNode.aabb);
        //float currentCost = 2 * node.aabb.GetSurfaceArea();
        float combinedCost = 2 * combinedAABB.GetSurfaceArea();

        float leftCost = AABB.CreateByAABB(node.left.aabb, newNode.aabb).GetSurfaceArea() + combinedCost - node.left.aabb.GetSurfaceArea();
        float rightCost = AABB.CreateByAABB(node.right.aabb, newNode.aabb).GetSurfaceArea() + combinedCost - node.right.aabb.GetSurfaceArea();

        if (leftCost < rightCost)
        {
            InsertNode(node.left, newNode);
        }
        else
        {
            InsertNode(node.right, newNode);
        }
    }
}

节点的删除 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

private void RemoveNode(Node node, GameObject obj)
{
    if (node == null)
    {
        return;
    }
    if (node.gameObject == obj)
    {
        if (node.isLeaf)
        {
            if (node == root)
            {
                root = null;
                node.parent = null;
                return;
            }
            else if (node.parent.left == node)
            {
                node.parent.left = null;
            }
            else
            {
                node.parent.right = null;
            }
        }
        
        Node parent = node.parent;
        while (parent != null)
        {
            if (parent.left != null && parent.right != null)
            {
                parent.aabb = AABB.CreateByAABB(parent.left.aabb, parent.right.aabb);
            }
            else if (parent.left != null)
            {
                parent.aabb = new AABB(parent.left.aabb.bounds);
            }
            else if (parent.right != null)
            {
                parent.aabb = new AABB(parent.right.aabb.bounds);
            }
            else {
                if (parent.parent!=null) {
                    if (parent.parent.left == parent)
                    {
                        parent.parent.left = null;
                    }
                    else {
                        parent.parent.right = null;
                    }
                }
            }
            parent = parent.parent;
        }
    }
    else
    {
        if (node.isLeaf == false)
        {
            RemoveNode(node.left, obj);
            RemoveNode(node.right, obj);
        }
    }
}
节点的更新 
1
2
3
4
5
6
7
8

public void UpdateObject(GameObject obj)
{
    RemoveObject(obj);
    AddObject(obj);
    return;
}

层次包围盒树的应用

1.碰撞检测

在Bullet、Havok等物理引擎的碰撞粗测阶段，使用一种叫做 动态层次AABB包围盒树(Dynamic Bounding Volume Hierarchy Based On AABB Tree) 的结构来存储动态的AABB形状。
然后通过该包围盒树的性质（不同父包围盒必定不会碰撞），快速过滤大量不可能发生碰撞的形状对

2.射线检测/挑选几何体

射线检测从层次包围盒树自顶向下检测是否射线通过包围盒，若不通过则无需检测其子包围盒。
这种剪裁可让每次射线检测平均只需检测O(logN)数量的形状。
通过一个点位置快速挑选该点的几何体也是类似的原理

3.视锥剔除

对BVH树进行中序遍历的视锥测试，如果一个节点所代表的包围盒不在视锥范围内，那么其所有子节点所代表的包围盒都不会在视锥范围内，则可以跳过测试其子节点。在这个遍历过程中，通过测试的节点所代表的几何体才可以发送渲染命令

4.光线追踪过滤

光线追踪渲染，可使用BVH来进行基于物体的划分，这样光线测试也可以过滤掉大量不必要的碰撞物体，效率一般比基于空间的划分还要好上一些

101中的部分截图

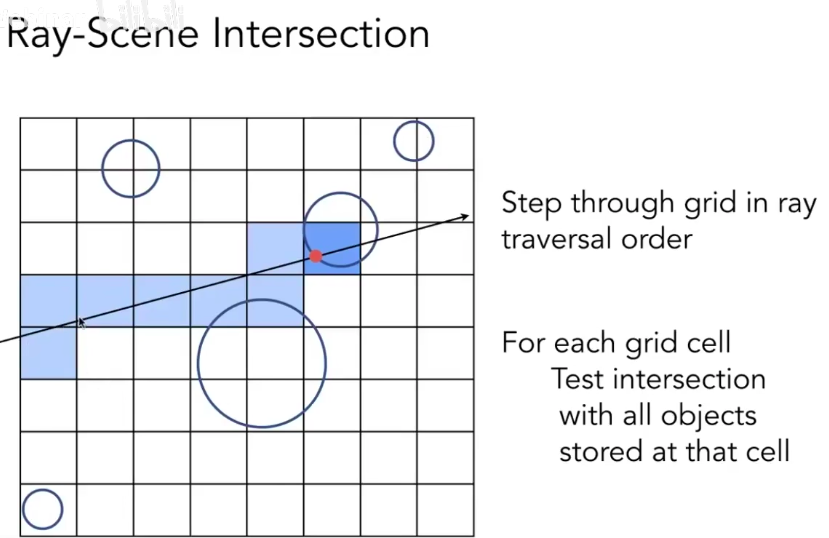
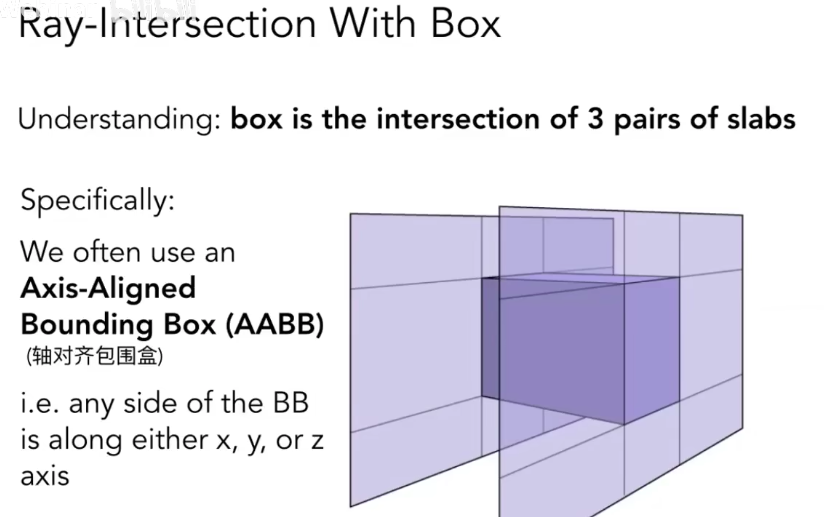
Image text
Image text

Image text
Image text
Image text

通过BVH(aabb)在光线追踪中过滤物体

AABB核心代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

#ifndef AABB_H
#define AABB_H

#include "rtweekend.h"

class aabb {
    public:
        point3 minimum;
        point3 maximum;

        aabb() {}
        aabb(const point3& a, const point3& b) { minimum = a; maximum = b;}

        point3 min() const {return minimum; }
        point3 max() const {return maximum; }

        virtual bool hit(const ray& r, double t_min, double t_max) const =0;

		//计算包裹两个包围盒的大包围盒
		aabb surrounding_box(aabb box0,aabb box1){
			point3 small(fmin(box0.min().x(), box1.min().x()),
						fmin(box0.min().y(), box1.min().y()),
						fmin(box0.min().z(), box1.min().z()));

			point3 big(fmax(box0.max().x(), box1.max().x()),
					fmax(box0.max().y(), box1.max().y()),
					fmax(box0.max().z(), box1.max().z()));

			return aabb(small,big);
		}
};

//检测射线和AABB的碰撞
inline bool aabb::hit(const ray& r, double t_min, double t_max) const {
    for (int a = 0; a < 3; a++) {
        auto invD = 1.0f / r.direction()[a];
        auto t0 = (min()[a] - r.origin()[a]) * invD;
        auto t1 = (max()[a] - r.origin()[a]) * invD;
        if (invD < 0.0f)
            std::swap(t0, t1);
        t_min = t0 > t_min ? t0 : t_min;
        t_max = t1 < t_max ? t1 : t_max;
        if (t_max <= t_min)
            return false;
    }
    return true;
}

#endif

BVH核心代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116

#ifndef BVH_H
#define BVH_H

#include "rtweekend.h"

#include "hittable.h"
#include "hittable_list.h"


class bvh_node : public hittable {
    public:
        bvh_node();

        bvh_node(const hittable_list& list, double time0, double time1)
            : bvh_node(list.objects, 0, list.objects.size(), time0, time1)
        {}

        bvh_node(
            const std::vector<shared_ptr<hittable>>& src_objects,
            size_t start, size_t end, double time0, double time1);

        virtual bool hit(
            const ray& r, double t_min, double t_max, hit_record& rec) const override;

        virtual bool bounding_box(double time0, double time1, aabb& output_box) const override;

    public:
        shared_ptr<hittable> left;
        shared_ptr<hittable> right;
        aabb box;
};

bool bvh_node::bounding_box(double time0, double time1, aabb& output_box) const {
    output_box = box;
    return true;
}

//返回最近的碰撞信息，如果有节点成功，则为true
bool bvh_node::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
    if (!box.hit(r, t_min, t_max))
        return false;

    bool hit_left = left->hit(r, t_min, t_max, rec);
    bool hit_right = right->hit(r, t_min, hit_left ? rec.t : t_max, rec);

    return hit_left || hit_right;
}

inline bool box_compare(const shared_ptr<hittable> a, const shared_ptr<hittable> b, int axis) {
    aabb box_a;
    aabb box_b;

    if (!a->bounding_box(0,0, box_a) || !b->bounding_box(0,0, box_b))
        std::cerr << "No bounding box in bvh_node constructor.\n";

    return box_a.min().e[axis] < box_b.min().e[axis];
}


bool box_x_compare (const shared_ptr<hittable> a, const shared_ptr<hittable> b) {
    return box_compare(a, b, 0);
}

bool box_y_compare (const shared_ptr<hittable> a, const shared_ptr<hittable> b) {
    return box_compare(a, b, 1);
}

bool box_z_compare (const shared_ptr<hittable> a, const shared_ptr<hittable> b) {
    return box_compare(a, b, 2);
}

//Bvh树的构建
bvh_node::bvh_node(
    std::vector<shared_ptr<hittable>>& src_objects,
    size_t start, size_t end, double time0, double time1
) {
    auto objects = src_objects; // Create a modifiable array of the source scene objects

    int axis = random_int(0,2);
    auto comparator = (axis == 0) ? box_x_compare
                    : (axis == 1) ? box_y_compare
                                  : box_z_compare;

    size_t object_span = end - start;

    if (object_span == 1) {
        left = right = objects[start];
    } else if (object_span == 2) {
        if (comparator(objects[start], objects[start+1])) {
            left = objects[start];
            right = objects[start+1];
        } else {
            left = objects[start+1];
            right = objects[start];
        }
    } else {
        std::sort(objects.begin() + start, objects.begin() + end, comparator);

        auto mid = start + object_span/2;
        left = make_shared<bvh_node>(objects, start, mid, time0, time1);
        right = make_shared<bvh_node>(objects, mid, end, time0, time1);
    }

    aabb box_left, box_right;

    if (  !left->bounding_box (time0, time1, box_left)
       || !right->bounding_box(time0, time1, box_right)
    )
        std::cerr << "No bounding box in bvh_node constructor.\n";

    box = surrounding_box(box_left, box_right);
}

#endif

5.辅助BSP树的构建

在BSP树的构建中，利用球体树辅助，可以将复杂度从O(Nlog^2^N)下降为O(NlogN)的复杂度

BSP树

随时渲染硬件的进步，基于BSP树的渲染慢慢淘汰。但是即使在今天，BSP仍是在其他分支（引擎编辑器）不可或缺的一个重要数据结构
在计算机图形学中以两种明显不同的形式存在，轴对齐树、多边形对齐树
BSP tree在3D空间下其每个节点表示一个平面，其代表的平面将当前空间划分为前向和背向两个子空间，分别对应左儿子和右儿子。
2D空间下，BSP树每个节点则表示一条边，也可以将2D空间划分成前后两部分

多边形对齐BSP

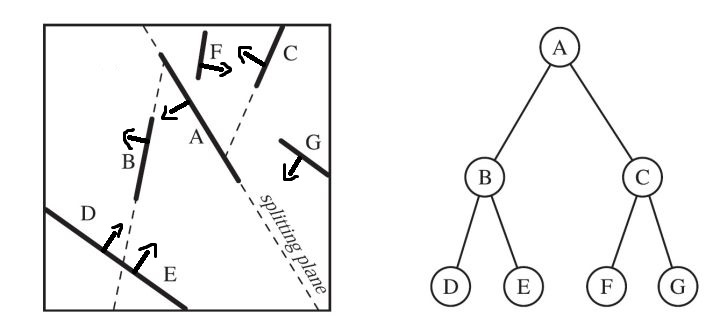
Image text

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
public class BSPTree
{
    private int m_MaxIteration;
    private int m_NodeCapacity;

    public List<BSPTreeNode> m_Nodes = new List<BSPTreeNode>();

    public void Divide(IList<float2> _points,out G2Plane _plane,out List<float2> _front,out List<float2> _back)
    {
        UPrincipleComponentAnalysis.Evaluate(_points,out var centre,out var right,out var up);
        _plane = new G2Plane(up,centre);
        _front = new List<float2>();
        _back = new List<float2>();
        foreach (var point in _points)
        {
            if(_plane.IsPointFront(point))
                _front.Add(point);
            else
                _back.Add(point);
        }
    }
    
    public void Construct(IList<float2> _points, int _maxIteration, int _nodeCapacity)
    {
        m_Nodes.Clear();
        m_Nodes.Add(new BSPTreeNode()
        {
            m_Iteration = 0,
            m_Plane = G2Plane.kDefault,
            m_Points = new List<float2>(_points),
        });
        
        bool doBreak = true;
        while (doBreak)
        {
            bool splited = false;
            for (int i = 0; i < m_Nodes.Count; i++)
            {
                var node = m_Nodes[i];
                if (node.m_Iteration >= _maxIteration)
                    continue;
                
                if (node.m_Points.Count < _nodeCapacity)
                    continue;

                Divide(node.m_Points,out var dividePlane,out var frontPoints,out var backPoints);
                
                m_Nodes.Add(new BSPTreeNode()
                {
                    m_Iteration = node.m_Iteration + 1,
                    m_Plane = dividePlane,
                    m_Points = frontPoints,
                    front = true,
                });
                
                m_Nodes.Add(new BSPTreeNode()
                {
                    m_Iteration = node.m_Iteration + 1,
                    m_Plane = dividePlane,
                    m_Points = backPoints,
                    front = false,
                });
                
                m_Nodes.RemoveAt(i);
                splited = true;
                break;
            }
            
            doBreak = splited;
        }
    }

    public void DrawGizmos()
    {
        int index = 0;
        var matrix = Gizmos.matrix;
        foreach (var node in m_Nodes)
        {
            Gizmos.color = UColor.IndexToColor(index++ % 6);
            Gizmos.matrix = matrix;
            foreach (var point in node.m_Points)
                Gizmos.DrawWireSphere(point.to3xz(),.1f);

            if (node.front)
            {
                Gizmos.matrix = matrix * Matrix4x4.TRS(node.m_Plane.position.to3xz(),Quaternion.LookRotation(node.m_Plane.normal.to3xz()),Vector3.one );
                Gizmos.DrawWireCube(Vector3.zero,(Vector3.right + Vector3.up)*5f);
                UGizmos.DrawString(Vector3.zero, node.m_Iteration.ToString());
            }
        }

        Gizmos.matrix = matrix;
    }
}


public static class UPrincipleComponentAnalysis
{
    public static void Evaluate(IEnumerable<float3> _points,out float3 _centre, out float3 _right, out float3 _up, out float3 _forward)
    {
        _right = kfloat3.right;
        _up = kfloat3.up;
        _forward = kfloat3.forward;

        var m = _points.Average();
        var a00 = 0f;
        var a11 = 0f;
        var a22 =0f;
        var a01mirror = 0f;
        var a02mirror = 0f;
        var a12mirror = 0f;
        int count = 0;
        foreach (var p in _points)
        {
            count++;
            a00+=umath.pow2(p.x - m.x);
            a11+=umath.pow2(p.y - m.y);
            a22+=umath.pow2(p.z - m.z);

            a01mirror += (p.x - m.x)*(p.y-m.y);
            a02mirror += (p.x - m.x)*(p.z-m.z);
            a12mirror += (p.y - m.y)*(p.z-m.z);
        }
        var matrix =  new float3x3(a00,a01mirror,a02mirror,
                                            a01mirror,a11,a12mirror,
                                                a02mirror,a12mirror,a22)/count;
        _centre = m;
        matrix.GetEigenVectors(out _right,out _up,out _forward);
    }

    public static void Evaluate(IList<float2> _points,out float2 _centre, out float2 _R, out float2 _S)
    {
        _R = kfloat2.up;
        _S = kfloat2.right;

        _centre = _points.Average();
        var m = _centre;
        var a00 = _points.Average(p => umath.pow2(p.x - m.x));
        var a11 = _points.Average(p => umath.pow2(p.y - m.y));
        var a01mirror = _points.Average(p => (p.x - m.x)*(p.y-m.y));
        new float2x2(a00,a01mirror,a01mirror,a11).GetEigenVectors(out _R,out _S);
    }
}
这段代码的理论基础涉及到主成分分析（Principal Component Analysis，PCA）。PCA 是一种常用的数据降维和特征提取方法，它通过找到数据的主要方向（主成分）来揭示数据的内在结构。
具体来说，这段代码使用了以下步骤：
1.计算均值 (m): 通过计算输入点集的均值，找到点集的中心。
2.计算协方差矩阵 (matrix): 使用每个点与均值的差值构建协方差矩阵。协方差矩阵描述了不同维度之间的关系，即数据的分散情况。
3.获取特征向量 (_right, _up, _forward): 通过求解协方差矩阵的特征向量，找到数据分布的主要方向。特征向量表示数据在新坐标系中的方向，而特征值则表示数据在相应方向上的方差。
4.输出结果 (_centre, _right, _up, _forward): 将中心点和主方向向量作为输出，这些向量可用于描述数据的形状和分布。
总的来说，PCA 的核心思想是通过找到数据中方差最大的方向，以及与之正交的次要方向，来描述数据的主要特征。在这个代码中，通过计算协方差矩阵的特征向量，实现了对数据分布主方向的提取

多边形对齐的BSP树有一些有用的属性。 一个是，对于给定的视图，树结构可以严格从后到前(或从前到后)遍历。 这与轴对齐的BSP树相比，后者通常只给出粗略排序的顺序。 确定相机位于根平面的哪一边。 在这个远平面的多边形集合在平表面的集合之外。 对于远平面，采取下一层的划分平面，并确定相机在哪一边。 远平面的子集也是离摄像机最远的子集。 通过继续递归，这个过程建立了严格的前后顺序，可以使用画家的算法来渲染场景。 画家的算法不需要z缓冲区。 如果所有对象都是按照前后顺序绘制的，那么每一个较近的对象就会被画在它后面的对象的前面，这样就不需要z-depth比较了。
link

轴对齐BSP树(K-D树)


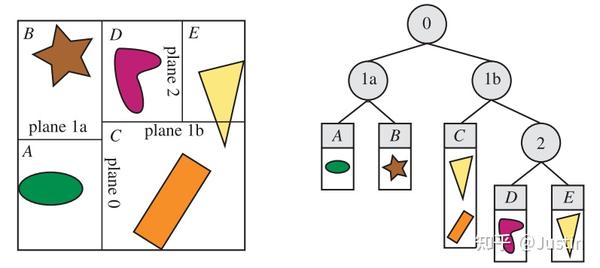
整个场景被包围在一个轴对齐的包围盒(AABB)中。 接下来的想法是递归地将这个包围盒划分为更小的包围盒
粗略的前后排序是如何使用轴对齐BSP树的一个例子。 这对于遮挡剔除算法是有用的(章节19.7和23.7)，以及通过最小化像素overdraw来减少像素着色器成本。 假设当前遍历一个名为N的节点。 这里，N是遍历开始时的根。 检查N的分割平面，然后递归地在查看器所在平面的一侧继续遍历树。 因此，只有当整个树的一半被遍历时，我们才开始遍历另一边。 由于叶节点的内容没有排序，而且对象可能位于树的许多节点中，因此这种遍历不会给出精确的前后排序。 然而，它给出了一个粗略的排序，这通常是有用的。 与观察者的位置相比，从节点平面的另一侧开始遍历，可以得到粗略的前后排序。 这对于透明排序很有用。 BSP遍历也可以用来测试光线对场景几何的影响，射线的位置只是用来交换观察者的位置
link

K-DOP

KSP的一种
UE4 K-DOP
AssetStore
Image Text

k-DOP是一种包围体，是K离散导向多面体（K discrete oriented polytope）的缩写，它是沿着K个方向的范围的布尔交集(zhuanlan.zhihu.com)(docs.unrealengine.com)。也就是说，一个k-DOP是k个包围平板的布尔交集，是一个包含对象的凸多面体（在2-D中是多边形，在3-D中是多面体）(en.wikipedia.org)。

要构建一个k-DOP，首先要选择k个方向，通常是沿着主轴或对角线的正负方向。然后，对于每个方向，计算对象上的所有顶点在该方向上的最小和最大投影值。这些值定义了沿着该方向的一个包围平板。最后，将所有的包围平板相交，得到一个k-DOP。

Bing大小姐给的代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# Assume obj is a list of vertices of the object
# Assume dot(v, n) is a function that computes the dot product of vector v and n
# Assume intersect(s1, s2) is a function that computes the intersection of two slabs s1 and s2
# Assume slab(n, min, max) is a function that creates a slab with normal n and min/max values along n
# Define the 26 directions as unit vectors
dirs = [(1, 0, 0), (-1, 0, 0), (0, 1, 0), (0, -1, 0), (0, 0, 1), (0, 0, -1),
    (1, 1, 0), (-1, -1, 0), (1, -1, 0), (-1, 1, 0),
    (1, 0, 1), (-1, 0, -1), (1, 0, -1), (-1, 0, 1),
    (0, 1, 1), (0, -1, -1), (0, 1, -1), (0, -1, 1),
    (sqrt(3)/3, sqrt(3)/3, sqrt(3)/3), (-sqrt(3)/3,-sqrt(3)/3,-sqrt(3)/3),
    (sqrt(3)/3,-sqrt(3)/3,-sqrt(3)/3), (-sqrt(3)/3,sqrt(3)/3,sqrt(3)/3),
    (sqrt(3)/3,sqrt(3)/3,-sqrt(3)/3), (-sqrt(3)/3,-sqrt(3)/3,sqrt(3)/3),
    (sqrt(3)/3,-sqrt(3)/3,sqrt(3)/3), (-sqrt(3)/3,sqrt(3)/3,-sqrt(3)/3)]
# Initialize the k-DOP as an empty list
kdop = []
# For each direction
for n in dirs:
    # Initialize the min and max values as infinity and negative infinity
    min = inf
    max = -inf
    # For each vertex of the object
    for v in obj:
        # Compute the projection value along n
        p = dot(v,n)
    # Update the min and max values if needed
    if p < min:
        min = p
    if p > max:
        max = p
    # Create a slab with normal n and min/max values along n
    s = slab(n,min,max)
    # Add the slab to the k-DOP
    kdop.append(s)
    # Intersect all the slabs in the k-DOP to get the final shape
    shape = kdop[0]
    for i in range(1,len(kdop)):
        shape = intersect(shape,kdop[i])
# Return the shape as the k-DOP
return
插件的思路

1.数据的定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
// Math.Sqrt(2)/2
private const float rcpSqrt2 = 0.70710678118f;
// Math.Sqrt(3)/3
private const float rcpSqrt3 = 0.57735026919f;


public static Vector3[] Dir10X = new Vector3[]
{
    new Vector3(1.0f, 0.0f, 0.0f),
    new Vector3(0.0f, 1.0f, 0.0f),
    new Vector3(0.0f, 0.0f, 1.0f),
    new Vector3(0.0f, rcpSqrt2, rcpSqrt2),
    new Vector3(0.0f, rcpSqrt2, -rcpSqrt2),
};

public static Vector3[] Dir10Y = new Vector3[]
{
    new Vector3(1.0f, 0.0f, 0.0f),
    new Vector3(0.0f, 1.0f, 0.0f),
    new Vector3(0.0f, 0.0f, 1.0f),
    new Vector3(rcpSqrt2, 0.0f, rcpSqrt2),
    new Vector3(rcpSqrt2, 0.0f, -rcpSqrt2),
};

public static Vector3[] KDopDir10Z = new Vector3[]
{
    new Vector3(1.0f, 0.0f, 0.0f),
    new Vector3(0.0f, 1.0f, 0.0f),
    new Vector3(0.0f, 0.0f, 1.0f),
    new Vector3(rcpSqrt2, rcpSqrt2, 0.0f),
    new Vector3(rcpSqrt2, -rcpSqrt2, 0.0f),
};

public static Vector3[] KDopDir18 = new Vector3[]
{
    new Vector3(1.0f, 0.0f, 0.0f),
    new Vector3(0.0f, 1.0f, 0.0f),
    new Vector3(0.0f, 0.0f, 1.0f),
    new Vector3(0.0f, rcpSqrt2, rcpSqrt2),
    new Vector3(0.0f, rcpSqrt2, -rcpSqrt2),
    new Vector3(rcpSqrt2, 0.0f, rcpSqrt2),
    new Vector3(rcpSqrt2, 0.0f, -rcpSqrt2),
    new Vector3(rcpSqrt2, rcpSqrt2, 0.0f),
    new Vector3(rcpSqrt2, -rcpSqrt2, 0.0f),
};

public static Vector3[] KDopDir26 = new Vector3[]
{
    new Vector3(1.0f, 0.0f, 0.0f),
    new Vector3(0.0f, 1.0f, 0.0f),
    new Vector3(0.0f, 0.0f, 1.0f),
    new Vector3(0.0f, rcpSqrt2, rcpSqrt2),
    new Vector3(0.0f, rcpSqrt2, -rcpSqrt2),
    new Vector3(rcpSqrt2, 0.0f, rcpSqrt2),
    new Vector3(rcpSqrt2, 0.0f, -rcpSqrt2),
    new Vector3(rcpSqrt2, rcpSqrt2, 0.0f),
    new Vector3(rcpSqrt2, -rcpSqrt2, 0.0f),
    new Vector3(rcpSqrt3, rcpSqrt3, rcpSqrt3),
    new Vector3(rcpSqrt3, -rcpSqrt3, rcpSqrt3),
    new Vector3(rcpSqrt3, rcpSqrt3, rcpSqrt3),
    new Vector3(-rcpSqrt3, -rcpSqrt3, rcpSqrt3),
};

2.核心功能

1
2
3
4
5
// Their either was no existing mesh or the user wanted to overwrite it,
// generate a new K-DOP

List<KDOPPolygon> polys = KDOPPolygon.GenerateKDopPolygons(gameObject.transform, meshFilters, dirs);
Mesh kdopMesh = KDOPPolygon.MeshFromPolygons(polys);

KDOPPolygon.GenerateTangentSpace

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

// Helper function to generate arbitrary tangent / bitangent for a given normal
private static void GenerateTangentSpace(Vector3 normal, out Vector3 tangent, out Vector3 bitangent)
{
    Vector3 N = new Vector3(Mathf.Abs(normal.x), Mathf.Abs(normal.y), Mathf.Abs(normal.z));

    // Find best basis vectors.
    if (N.z > N.x && N.z > N.y)
    {
        tangent = new Vector3(1, 0, 0);
    }
    else
    {
        tangent = new Vector3(0, 0, 1);
    }
    // 得到和法线想垂直的向量作为切线，normal取自预先设定好的数组，不需要进行 normalize()
    tangent = Vector3.Normalize(tangent - normal * Vector3.Dot(tangent, normal));
    bitangent = Vector3.Cross(tangent, normal);
}

KDOPPolygon.Split

方法中的参数planeOrigin表示平面的原点（一个点），planeNormal表示平面的法线方向（一个单位向量）。

首先，使用一个循环遍历多边形的所有边（由顶点Vertices[i]和Vertices[j]组成），并检查它们是否与平面相交。对于每条边，通过计算边向量t与平面法线的点积t_dot_n，来判断是否可能存在交点。如果点积的绝对值大于一个较小的阈值（1e-4f），表示存在可能的交点。

如果存在可能的交点，再计算交点参数d，通过计算平面原点到顶点Vertices[i]的向量与平面法线的点积，除以边向量t与平面法线的点积。如果d的值在0和1之间，表示交点在边上（不包括顶点），则在这个位置将交点插入到多边形的顶点列表中。

接下来，将平面原点沿着平面法线方向稍微向外偏移（planeOrigin -= planeNormal * 0.001f）。

最后，再次遍历多边形的顶点列表，将位于平面负（错误）一侧的顶点从列表中移除，即将多边形中位于平面错误一侧的部分去除。

这样，通过在给定平面上进行分割操作，可以将多边形切割为两个或更多部分，其中一部分位于平面的正（正确）一侧，另一部分位于平面的负（错误）一侧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
// 计算平面和线的交点
public static Vector3 CalculatePlaneLineIntersection(Vector3 planeNormal, Vector3 planePoint, Vector3 linePoint, Vector3 lineDirection)
{
    float dot = Vector3.Dot(planeNormal, lineDirection);

    // 如果线与平面平行，则没有交点
    if (Mathf.Approximately(dot, 0))
    {
        return Vector3.zero;
    }

    float t = Vector3.Dot(planeNormal, planePoint - linePoint) / dot;
    Vector3 intersectionPoint = linePoint + t * lineDirection;
    return intersectionPoint;
}

// Split this polygon at a plane. 
private void Split(Vector3 planeOrigin, Vector3 planeNormal)
{
    // Loop over all edges i..j and check whether they intersect the plane
    for (int i = 0; i < Vertices.Count; ++i)
    {
        int j = (i + 1) % Vertices.Count;

        Vector3 t = Vertices[j] - Vertices[i];
        float t_dot_n = Vector3.Dot(t, planeNormal);

        // Dot product != 0? Possible intersection 
        if (Mathf.Abs(t_dot_n) > 1e-4f)
        {
            //计算平面和线的交点
            //平面公式 Ax+By+Cz+D=0 (A\B\C)是法线向量的分量，D是-N·P(点)
            //线的公式 P=P0+tD
            //如果存在 t 值，说明有交点，0-1范围说明交点在线段上
            float d = Vector3.Dot(planeOrigin - Vertices[i], planeNormal) / t_dot_n;
            if (d > 0.0f && d < 1.0f)
            {
                Vertices.Insert(i + 1, d * t + Vertices[i]);
                ++i;
            }
        }
    }

    // Shift plane origin for clipping
    planeOrigin -= planeNormal * 0.001f;

    // Remove all vertices that are on the wrong side of the cutting plane
    for (int i = 0; i < Vertices.Count; ++i)
    {
        if (Vector3.Dot(Vertices[i] - planeOrigin, planeNormal) < 0.0f)
        {
            Vertices.RemoveAt(i);
            --i;
        }
    }
}

KDOPPolygon.GenerateKDopPolygons

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
// Generate the polygons for a K-DOP by iteratively intersecting planes with each other.
public static List<KDOPPolygon> GenerateKDopPolygons(Transform rootTransform, MeshFilter[] meshFilters, Vector3[] dirs)
{
    int planePairCount = dirs.Length;
    float[] minDist = new float[planePairCount];
    float[] maxDist = new float[planePairCount];
    for (int i = 0; i < planePairCount; i++)
    {
        minDist[i] = float.MaxValue;
        maxDist[i] = -float.MaxValue;
    }

    // Extents of the initial planes
    float PlaneExtents = 0.0f;

    // Loop over all meshes
    foreach (MeshFilter meshFilter in meshFilters)
    {
        // Choose a value well over the extents of the mesh for initial planes
        Mesh mesh = meshFilter.sharedMesh;
        Vector3[] vertices = mesh.vertices;
        PlaneExtents = Mathf.Max(PlaneExtents, 100.0f * Mathf.Max(mesh.bounds.extents.x, Mathf.Max(mesh.bounds.extents.y, mesh.bounds.extents.z)));

        // For each vertex, project along each K-DOP direction, to find max and min in that direction
        for (int i = 0; i < mesh.vertexCount; i++)
        {
            // We may be dealing with complex GameObjects here, so the root object may have a transform (which
            // will also be applied to the collision mesh and thus is to be ignored), and the children may have
            // a transform too (which is important to end up with a correct collision mesh for the compound
            // object). Let's deal with that.
            Vector3 vertex = vertices[i];
            vertex = meshFilter.transform.TransformPoint(vertex);
            vertex = rootTransform.InverseTransformPoint(vertex);

            for (int j = 0; j < planePairCount; j++)
            {
                float dist = Vector3.Dot(vertex, dirs[j]);
                minDist[j] = Mathf.Min(dist, minDist[j]);
                maxDist[j] = Mathf.Max(dist, maxDist[j]);
            }
        }
    }

    // Generate and split polygons
    List<KDOPPolygon> polys = new List<KDOPPolygon>();
    for (int i = 0; i < planePairCount; i++)
    {
        // Get tangent / bitangent
        Vector3 AxisX, AxisY;
        GenerateTangentSpace(dirs[i], out AxisX, out AxisY);

        // which 0: Positive (maximum) plane
        // which 1: Negative (minimum) plane
        for (int which = 0; which < 2; ++which)
        {
            // Create first polygon
            KDOPPolygon poly = new KDOPPolygon();
            poly.Normal = (which == 0 ? dirs[i] : -dirs[i]);

            if (Vector3.Dot(Vector3.Cross(AxisX, AxisY), poly.Normal) > 0.0f)
                AxisX *= -1;

            Vector3 baseP = dirs[i] * (which == 0 ? maxDist[i] : minDist[i]);
            poly.Vertices.Add(baseP + AxisX * PlaneExtents + AxisY * PlaneExtents);
            poly.Vertices.Add(baseP + AxisX * PlaneExtents - AxisY * PlaneExtents);
            poly.Vertices.Add(baseP - AxisX * PlaneExtents - AxisY * PlaneExtents);
            poly.Vertices.Add(baseP - AxisX * PlaneExtents + AxisY * PlaneExtents);

            for (int j = 0; j < planePairCount; j++)
            {
                if (i != j || which == 1) poly.Split(dirs[j] * maxDist[j], -dirs[j]);
                if (i != j || which == 0) poly.Split(dirs[j] * minDist[j], dirs[j]);
            }

            if (poly.Vertices.Count >= 3)
                polys.Add(poly);
        }
    }

    return polys;
}

KDOPPolygon.MeshFromPolygons
Mesh顶点数据生成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

// Generate a mesh from a list 
public static Mesh MeshFromPolygons(List<KDOPPolygon> polys)
{
    // Generate mesh
    List<Vector3> vertices = new List<Vector3>();
    List<int> indices = new List<int>();
    foreach (KDOPPolygon p in polys)
        p.ToTriangles(vertices, indices);

    Mesh mesh = new Mesh();
    mesh.vertices = vertices.ToArray();
    mesh.SetIndices(indices.ToArray(), MeshTopology.Triangles, 0);

    return mesh;
}

缓存敏感和缓存相关表示

19.1 空间数据结构 - Justin的文章 - 知乎