RayTracing

Shader
5.9k words

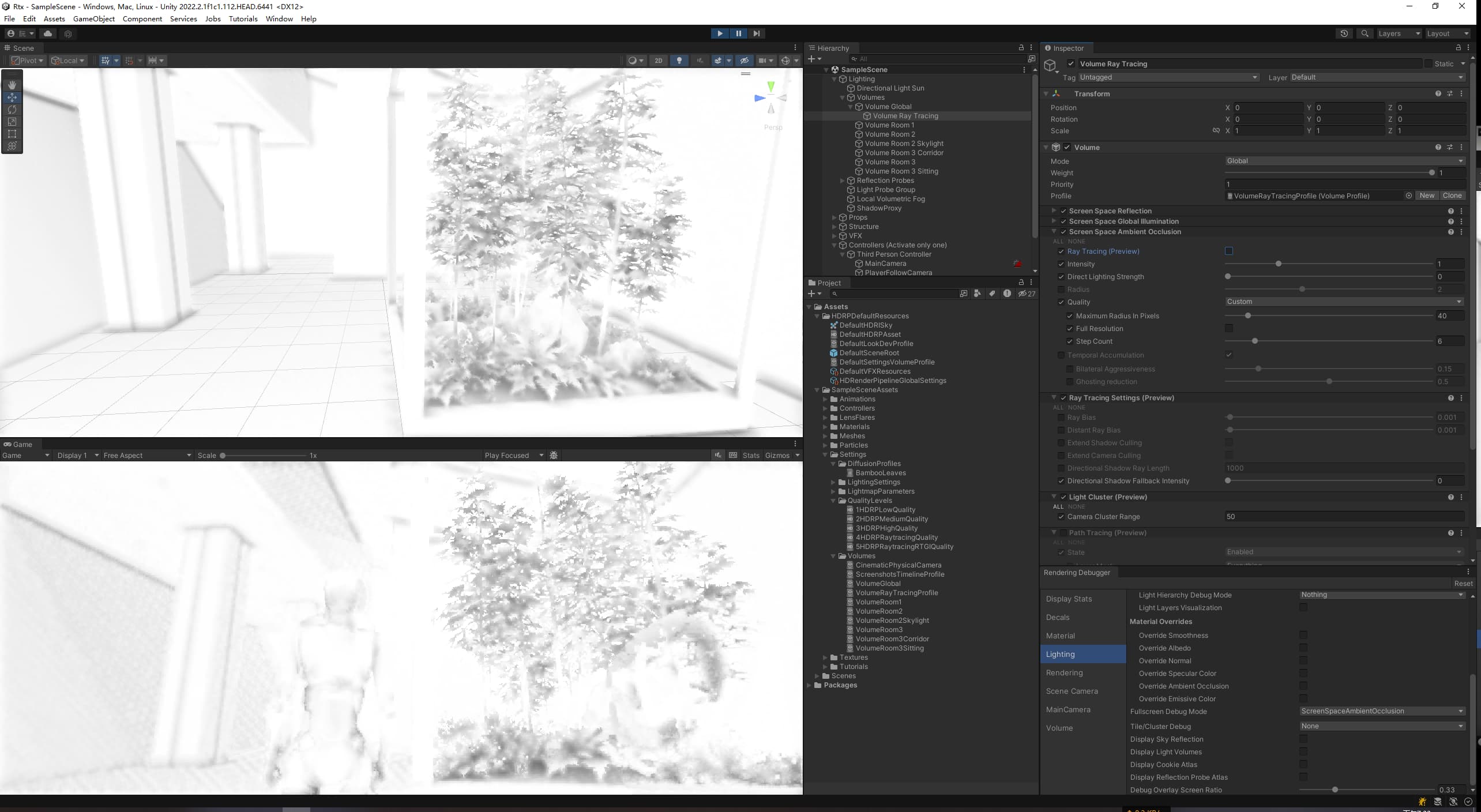
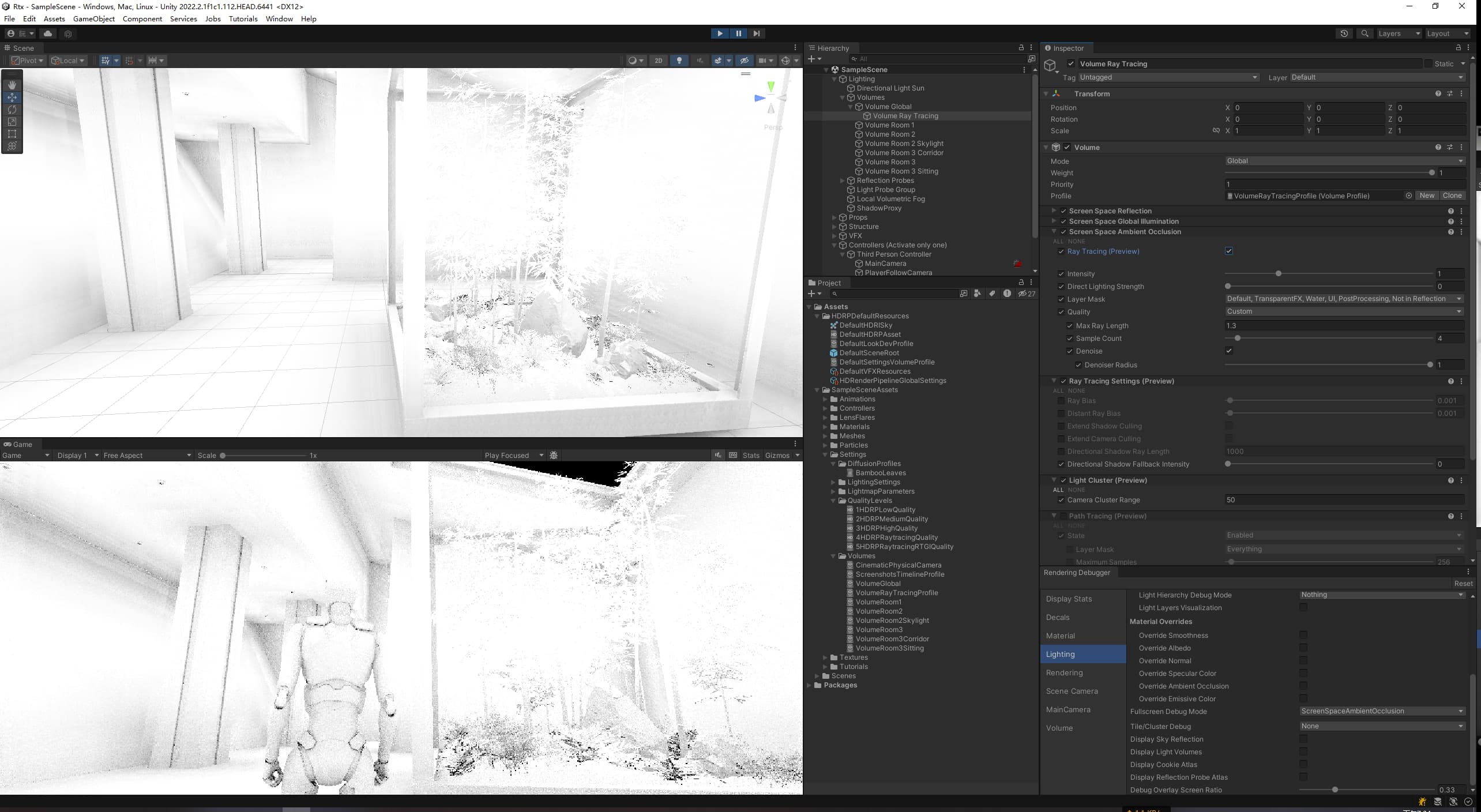
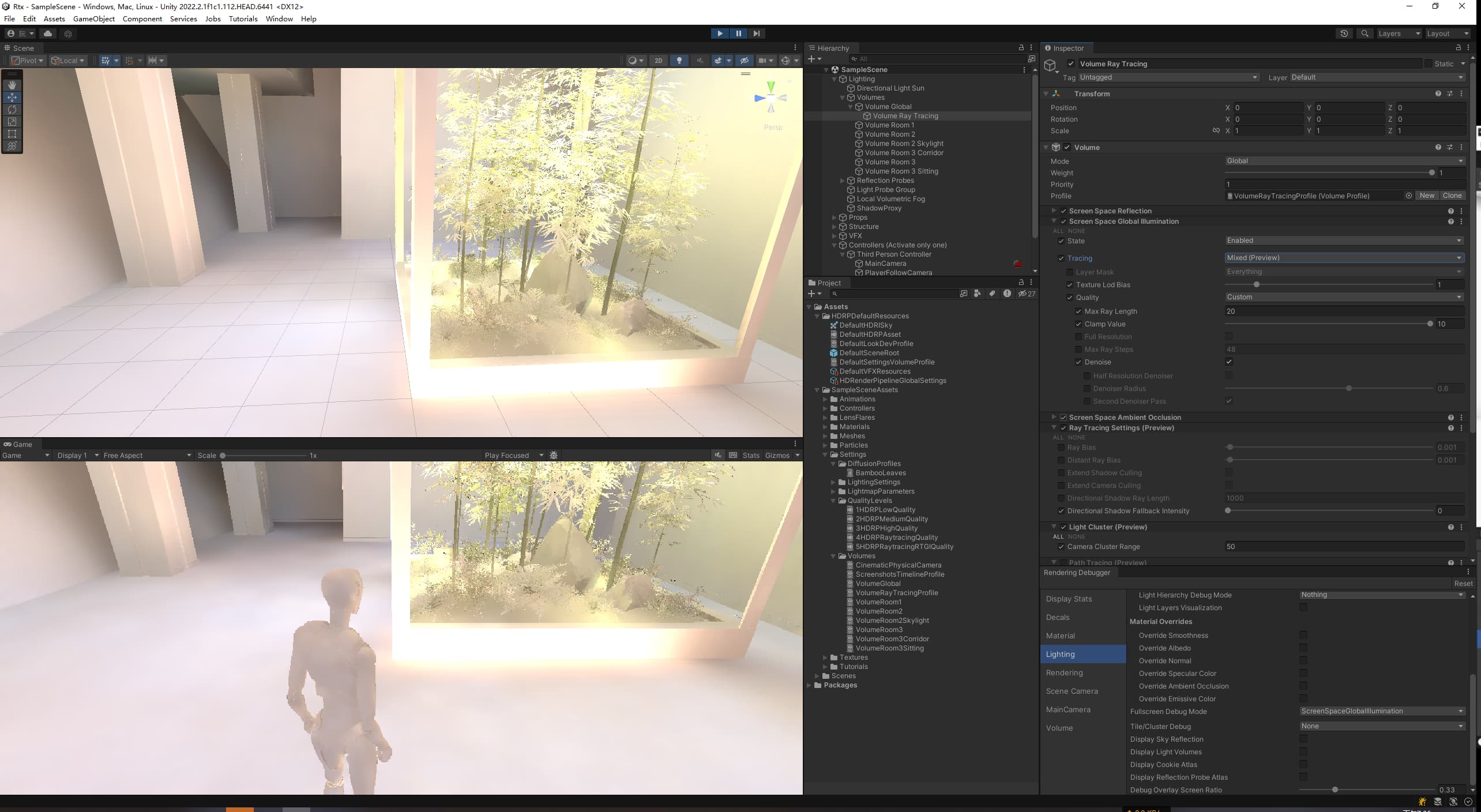
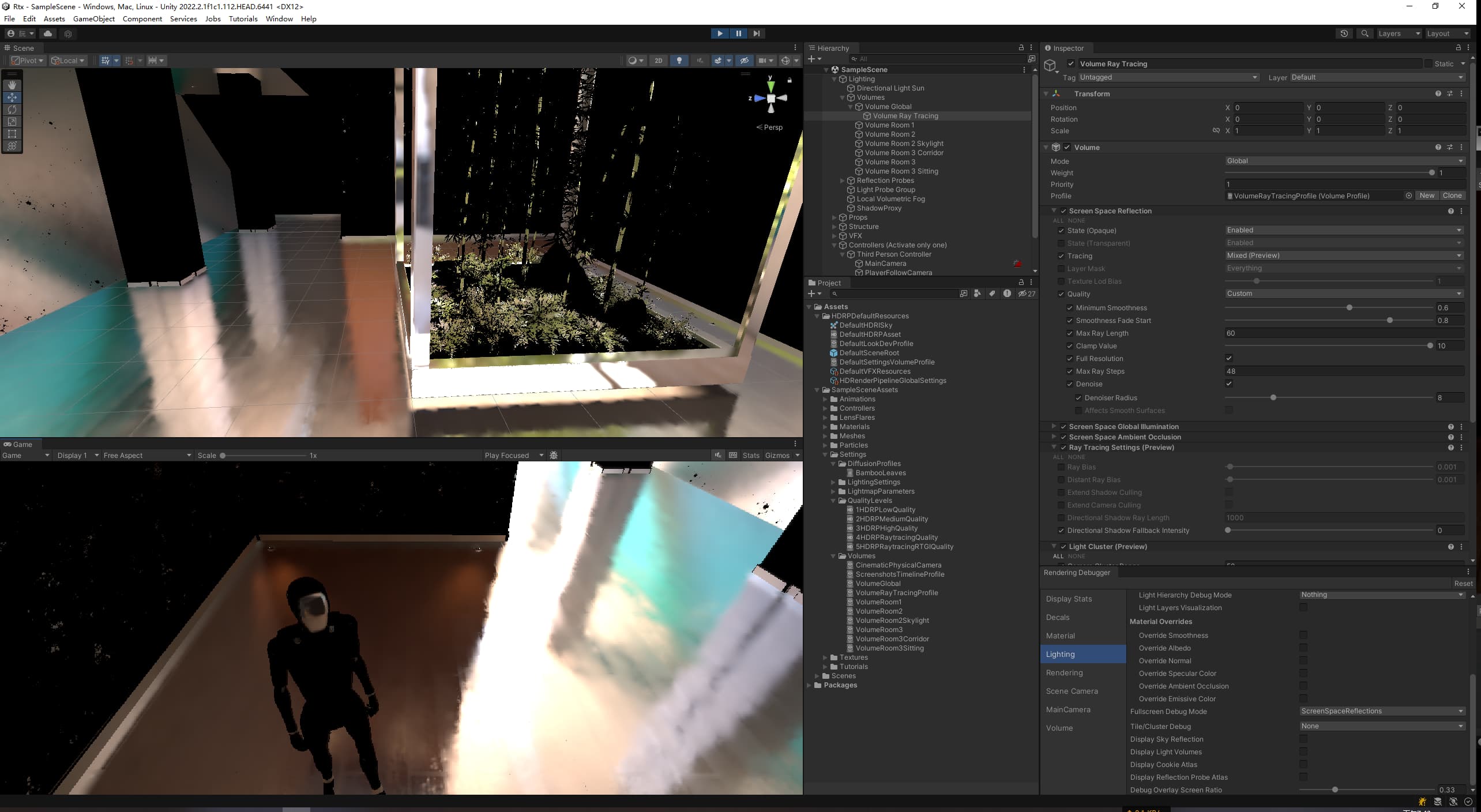
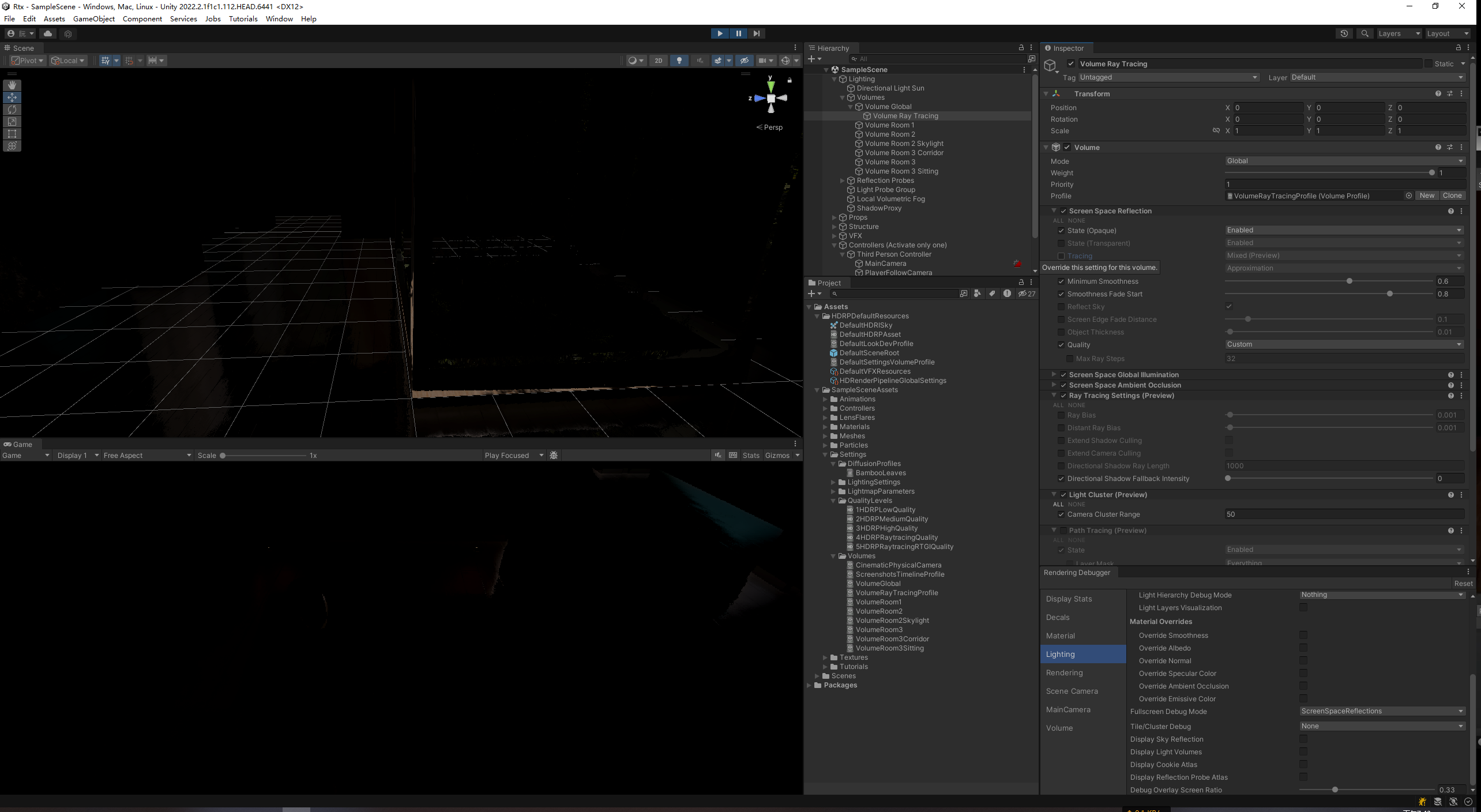
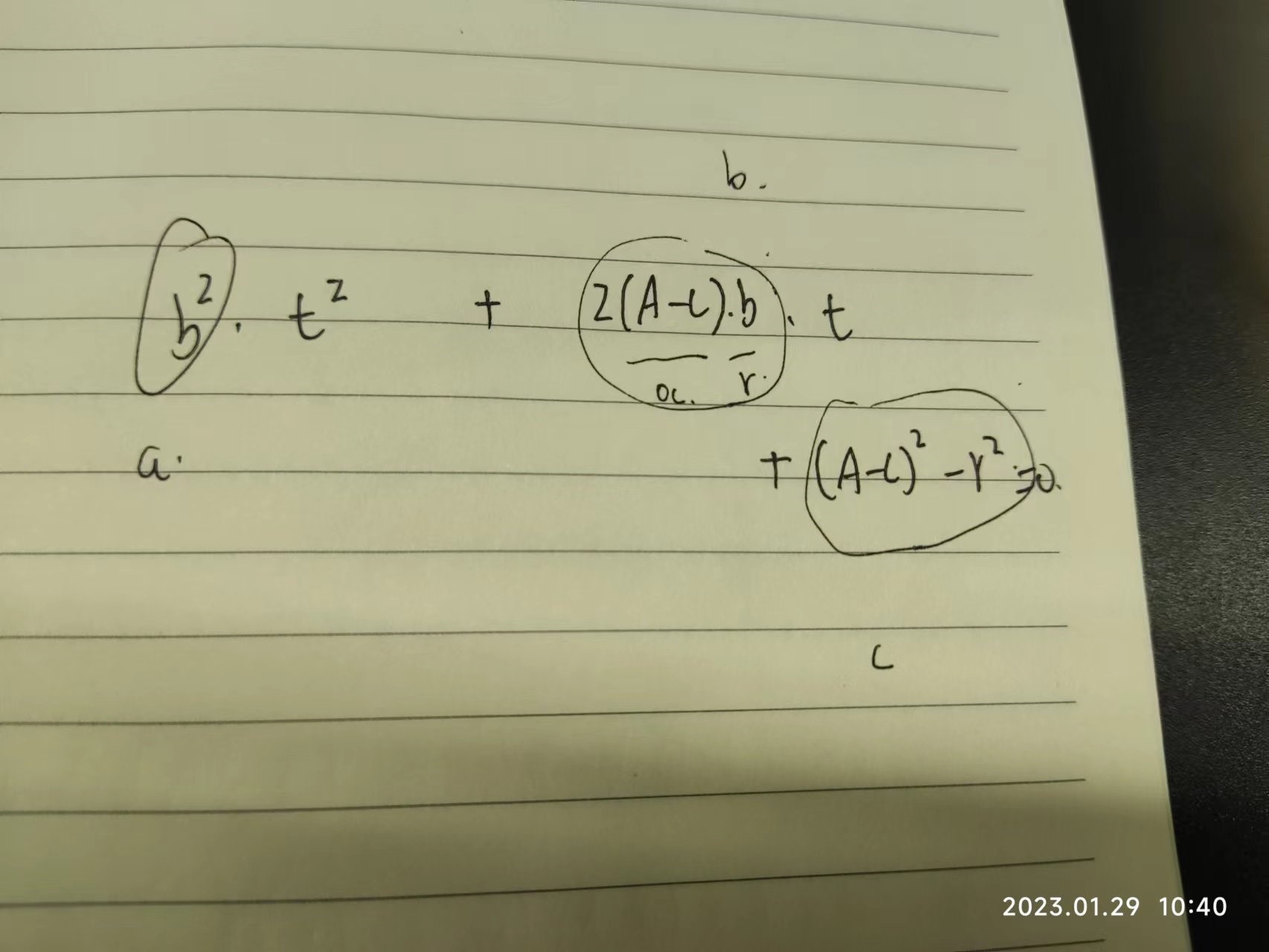Desc

用Unity2022的HDRP光追试了下，感觉效果挺好的，不过没看到20版本提到的步数

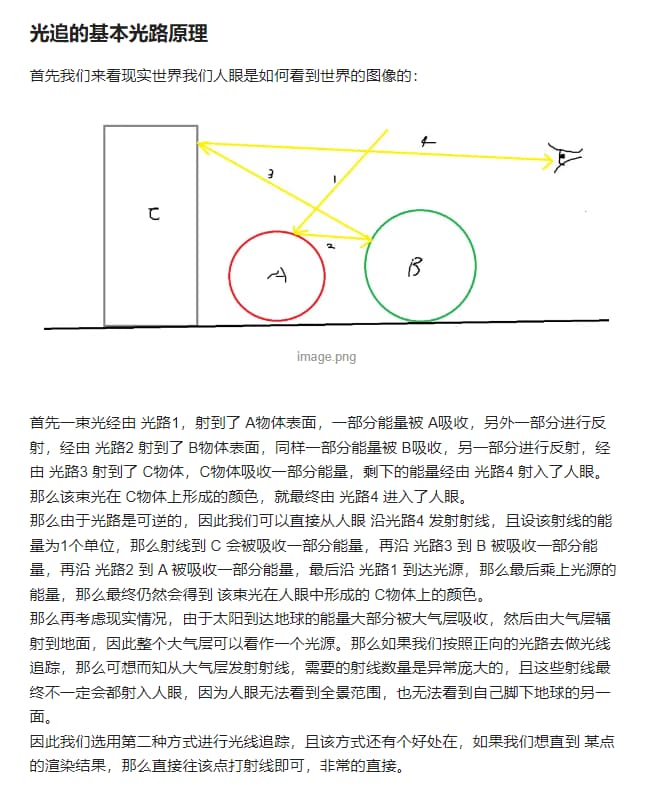
原理

根据光路可逆，从眼睛表面积分发出射线。
设射线的能量为1单位，射线到达物体时，会被吸收一部分能量，再沿着其他方向发射出去，如果到达光源，则最后乘上光源的能量

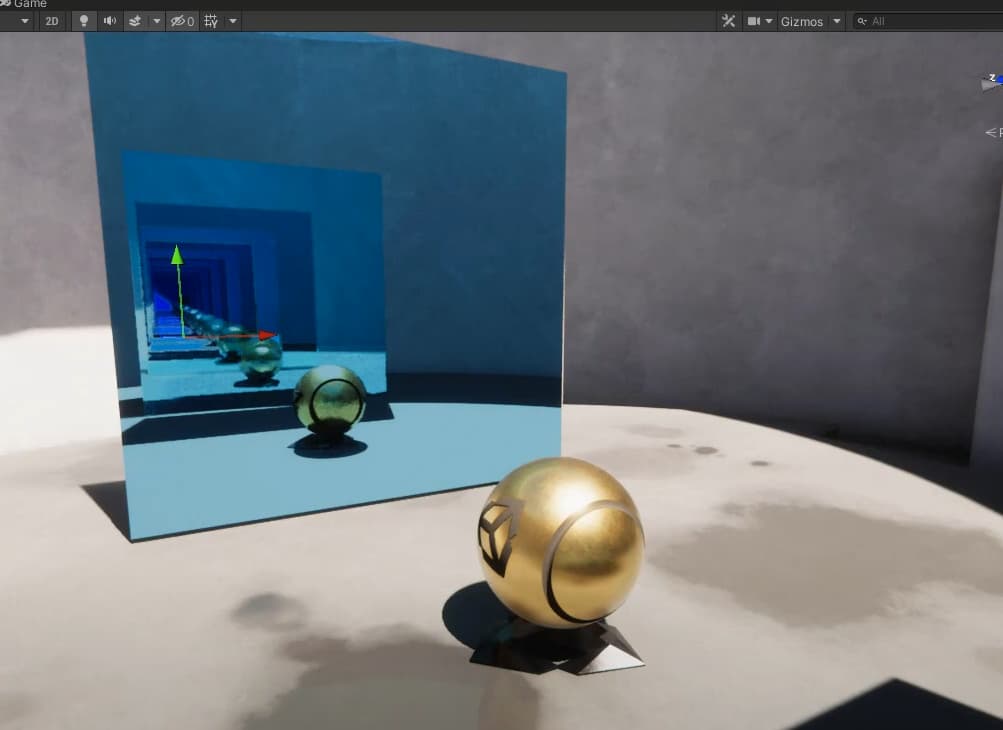
效果

效果图

没有开启光追的屏幕环境光遮罩
Image text
开启光追的环境光遮罩
Image text
屏幕空间全局光照
Image text
开启光追的屏幕空间反射
Image text
关闭光追后的结果
Image text
教程中演示的提高步数后的屏幕空间反射
Image text

链接

youtube

C++实现光线追踪

来源

link

ray

射线表达式，P(t)=A+tb
P:射线上的点
A:射线的起点
b:射线的方向向量
t:射线起点A到P的距离

判断射线和球体有无交点

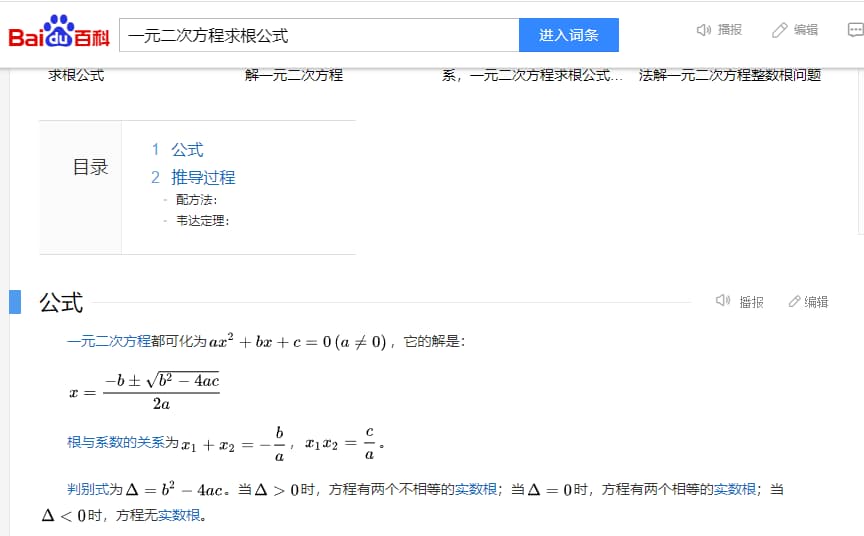
证明相关

Image text
Image text
Image text
Image text

1
2
3
4
5
6
7
8
9
10
11
12
13
double hit_sphere(const point3& center, double radius, const ray& r) {
    vec3 oc = r.origin() - center;
    auto a = dot(r.direction(), r.direction());
    auto b = 2.0 * dot(oc, r.direction());
    auto c = dot(oc, oc) - radius * radius;
    auto discriminant = b * b - 4 * a * c;
    if (discriminant < 0) {
        return -1;
    }
    else {
        return (-b - sqrt(discriminant)) / (2.0 * a);
    }
}
1
2
3
4
5
6
7
#交点的法线
auto t = hit_sphere(sphere_center, 0.5, r);
if (t>0) {
    vec3 N = unit_vector(r.at(t) - sphere_center);
    return 0.5 * color(N.x() + 1, N.y() + 1, N.z() + 1);
}

路径追踪原理

Image text
对于一个像素，可以发出多条射线，最后对射线结果取均值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void write_color(std::ostream& out, color pixel_color, int samples_per_pixel) {
	auto r = pixel_color.x();
	auto g = pixel_color.y();
	auto b = pixel_color.z();

	auto scale = 1.0 / samples_per_pixel;
	r *= scale;
	g *= scale;
	b *= scale;

	out << static_cast<int>(255 * clamp(r, 0, 0.999)) << ' '
		<< static_cast<int>(255 * clamp(g, 0, 0.999)) << ' '
		<< static_cast<int>(255 * clamp(b, 0, 0.999)) << '\n';
}

for (int j = image_heigth - 1; j >= 0; j--) {
    for (int i = 0; i < image_width; i++) {
        color pixel_color(0, 0, 0);
        for (int s = 0; s < samples_per_pixel; s++) {
            auto u = (i + random_double()) / (image_width - 1);
            auto v = (j + random_double()) / (image_heigth - 1);
            ray r = cam.get_ray(u,v);
            pixel_color += ray_color(r, world);
        }
        write_color(std::cout,pixel_color,samples_per_pixel);
    }
}

光线与物体相交的检测

Hittable(物体的基类，用于提供与射线碰撞的参数和接口定义) 
1
virtual bool hit(const ray& r, double t_min, double t_max, hit_record& rec) const = 0;
Sphere 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

bool sphere::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
    vec3 oc = r.origin() - center;
    auto a = r.direction().length_squared();
    auto half_b = dot(oc, r.direction());
    auto c = oc.length_squared() - radius*radius;

    auto discriminant = half_b*half_b - a*c;
    if (discriminant < 0) return false;
    auto sqrtd = sqrt(discriminant);

    // Find the nearest root that lies in the acceptable range.
    auto root = (-half_b - sqrtd) / a;
    if (root < t_min || t_max < root) {
        root = (-half_b + sqrtd) / a;
        if (root < t_min || t_max < root)
            return false;
    }

    rec.t = root;
    rec.p = r.at(rec.t);
    rec.normal = (rec.p - center) / radius;

    return true;
}

Hittable_list 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

bool hittable_list::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
    hit_record temp_rec;
    bool hit_anything = false;
    auto closest_so_far = t_max;

    for (const auto& object : objects) {
        if (object->hit(r, t_min, closest_so_far, temp_rec)) {
            hit_anything = true;
            closest_so_far = temp_rec.t;
            rec = temp_rec;
        }
    }

    return hit_anything;
}

Moving_sphere 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
bool moving_sphere::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
    vec3 oc = r.origin() - center(r.time());
    auto a = r.direction().length_squared();
    auto half_b = dot(oc, r.direction());
    auto c = oc.length_squared() - radius*radius;

    auto discriminant = half_b*half_b - a*c;
    if (discriminant < 0) return false;
    auto sqrtd = sqrt(discriminant);

    // Find the nearest root that lies in the acceptable range.
    auto root = (-half_b - sqrtd) / a;
    if (root < t_min || t_max < root) {
        root = (-half_b + sqrtd) / a;
        if (root < t_min || t_max < root)
            return false;
    }

    rec.t = root;
    rec.p = r.at(rec.t);
    auto outward_normal = (rec.p - center(r.time())) / radius;
    rec.set_face_normal(r, outward_normal);
    rec.mat_ptr = mat_ptr;

    return true;
}
AABB 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline bool aabb::hit(const ray& r, double t_min, double t_max) const {
    for (int a = 0; a < 3; a++) {
        auto invD = 1.0f / r.direction()[a];
        auto t0 = (min()[a] - r.origin()[a]) * invD;
        auto t1 = (max()[a] - r.origin()[a]) * invD;
        if (invD < 0.0f)
            std::swap(t0, t1);
        t_min = t0 > t_min ? t0 : t_min;
        t_max = t1 < t_max ? t1 : t_max;
        if (t_max <= t_min)
            return false;
    }
    return true;
}
Bvh_node 
1
2
3
4
5
6
7
8
9
bool bvh_node::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
    if (!box.hit(r, t_min, t_max))
        return false;

    bool hit_left = left->hit(r, t_min, t_max, rec);
    bool hit_right = right->hit(r, t_min, hit_left ? rec.t : t_max, rec);

    return hit_left || hit_right;
}
Rect 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
bool xy_rect::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
    auto t = (k-r.origin().z()) / r.direction().z();
    if (t < t_min || t > t_max)
        return false;
    auto x = r.origin().x() + t*r.direction().x();
    auto y = r.origin().y() + t*r.direction().y();
    if (x < x0 || x > x1 || y < y0 || y > y1)
        return false;
    rec.u = (x-x0)/(x1-x0);
    rec.v = (y-y0)/(y1-y0);
    rec.t = t;
    auto outward_normal = vec3(0, 0, 1);
    rec.set_face_normal(r, outward_normal);
    rec.mat_ptr = mp;
    rec.p = r.at(t);
    return true;
}

bool xz_rect::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
    auto t = (k-r.origin().y()) / r.direction().y();
    if (t < t_min || t > t_max)
        return false;
    auto x = r.origin().x() + t*r.direction().x();
    auto z = r.origin().z() + t*r.direction().z();
    if (x < x0 || x > x1 || z < z0 || z > z1)
        return false;
    rec.u = (x-x0)/(x1-x0);
    rec.v = (z-z0)/(z1-z0);
    rec.t = t;
    auto outward_normal = vec3(0, 1, 0);
    rec.set_face_normal(r, outward_normal);
    rec.mat_ptr = mp;
    rec.p = r.at(t);
    return true;
}

bool yz_rect::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
    auto t = (k-r.origin().x()) / r.direction().x();
    if (t < t_min || t > t_max)
        return false;
    auto y = r.origin().y() + t*r.direction().y();
    auto z = r.origin().z() + t*r.direction().z();
    if (y < y0 || y > y1 || z < z0 || z > z1)
        return false;
    rec.u = (y-y0)/(y1-y0);
    rec.v = (z-z0)/(z1-z0);
    rec.t = t;
    auto outward_normal = vec3(1, 0, 0);
    rec.set_face_normal(r, outward_normal);
    rec.mat_ptr = mp;
    rec.p = r.at(t);
    return true;
}

通过BVH实现过滤物体

BVH

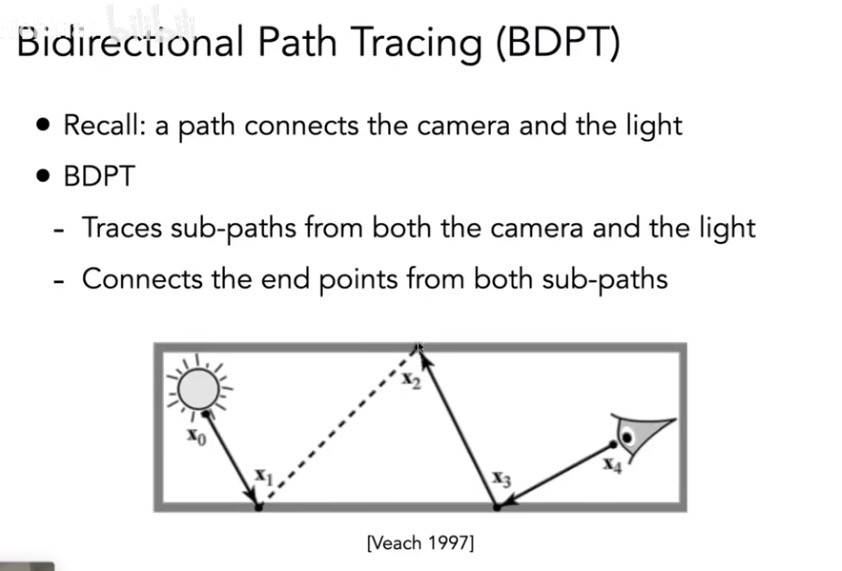
当前先进的光线追踪技术(Game101)

双向路径追踪（BDPT）

速度慢，但是针对大部分为间接光照时效果好

Image text
Image text

MLT

难以估算进度，每个像素的操作都是局部的，不同帧之间结果会不同

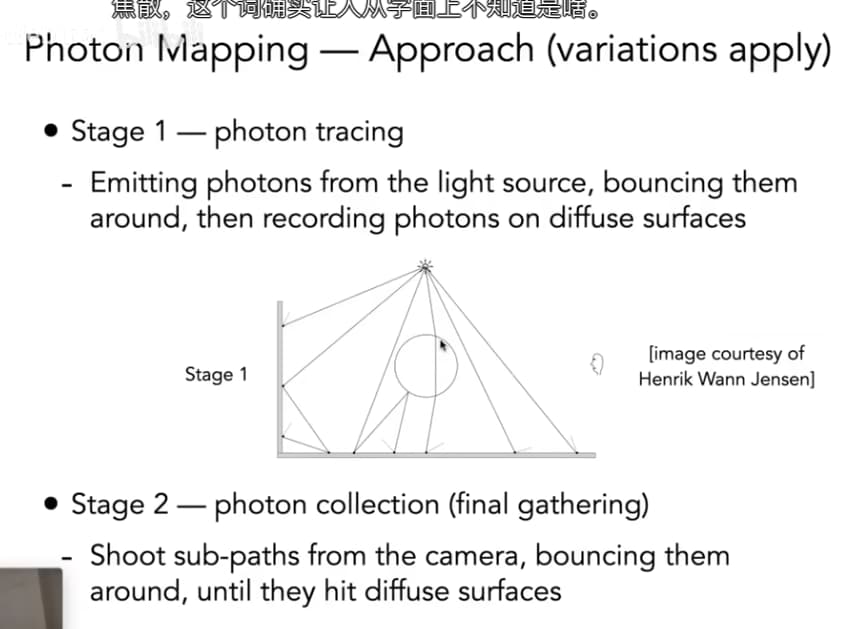
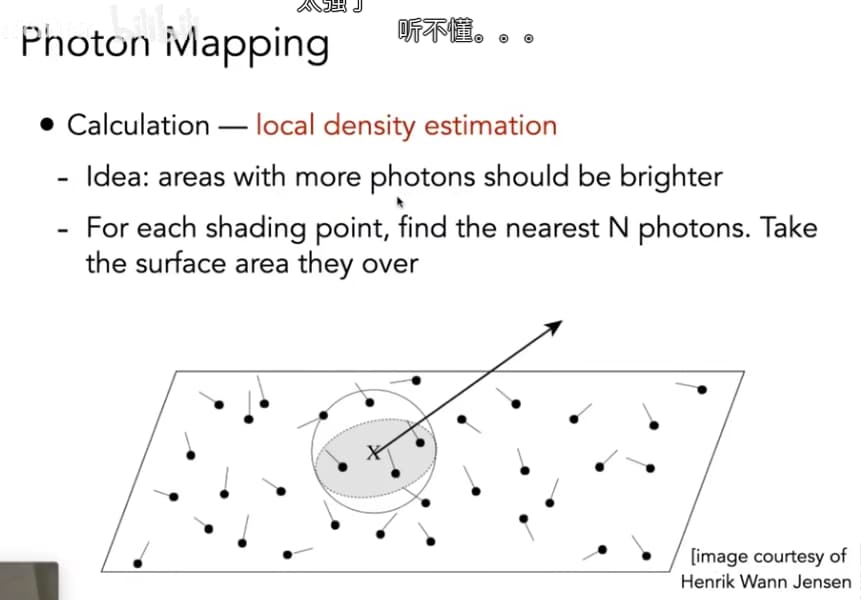
Image text
Image text

Photon Mapping

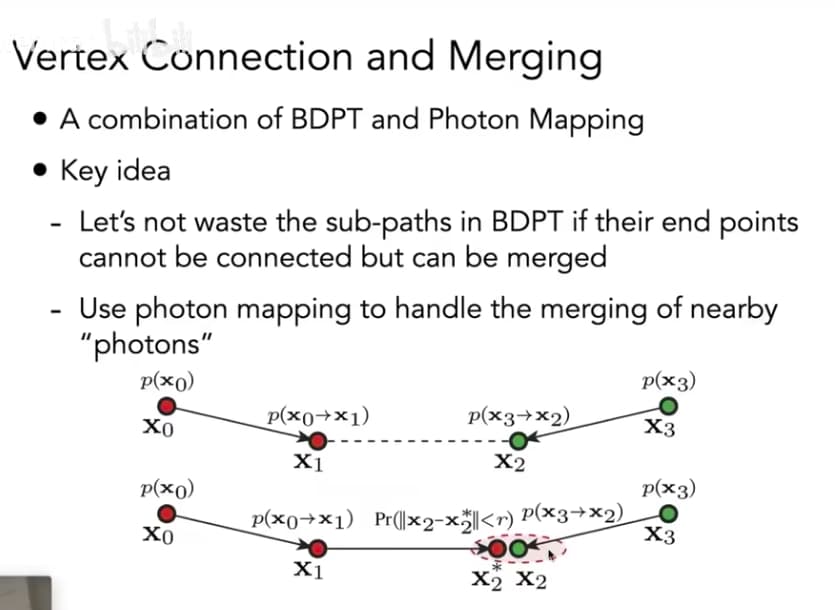
Image text
Image text
Image text
Image text
特比适合 Caustics(焦散？)

Vertex Connection and Merging

Image text
BDPT 和 Photon Mapping 的结合

Instant Radiosity

主光源反射后的间接光当作光源去计算
VPL不能处理镜面物体
Image text